题目内容
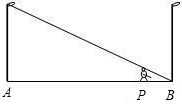 如图,小亮同学在晚上由路灯A走向路灯B,当他走到点P时,发现他的身影顶部正好接触路灯B的底部,这时他离路灯A25米,离路灯B5米,如果小亮的身高为1.6米,那么路灯高度为
如图,小亮同学在晚上由路灯A走向路灯B,当他走到点P时,发现他的身影顶部正好接触路灯B的底部,这时他离路灯A25米,离路灯B5米,如果小亮的身高为1.6米,那么路灯高度为分析:如图,要求路灯的高度AC,可以利用△BPQ∽△BAC,由它们的对应边成比例就可以求出.
解答: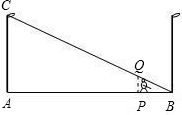 解:如图,依题意有PQ∥CA.
解:如图,依题意有PQ∥CA.
∴△BPQ∽△BAC
∴
=
而PQ=1.6,PB=5,PA=25,AB=PA+PB=25+5=30.
∴
=
∴AC=9.6
∴路灯的高度为9.6米.
 解:如图,依题意有PQ∥CA.
解:如图,依题意有PQ∥CA.∴△BPQ∽△BAC
∴
| PQ |
| AC |
| PB |
| BA |
而PQ=1.6,PB=5,PA=25,AB=PA+PB=25+5=30.
∴
| 1.6 |
| AC |
| 5 |
| 30 |
∴AC=9.6
∴路灯的高度为9.6米.
点评:本题考查相似三角形性质的应用.解题时关键是找出相似的三角形然后利用它们的对应边成比例就可以求出.

练习册系列答案
相关题目
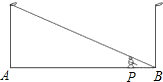 如图,小亮同学在晚上由路灯A走向路灯B,当他走到点P时,发现他的身影顶部正好接触路灯B的底部,这时他离路灯A25米,离路灯B5米,如果小亮的身高为1.6米,那么路灯高度为( )
如图,小亮同学在晚上由路灯A走向路灯B,当他走到点P时,发现他的身影顶部正好接触路灯B的底部,这时他离路灯A25米,离路灯B5米,如果小亮的身高为1.6米,那么路灯高度为( )| A、6.4米 | B、8米 | C、9.6米 | D、11.2米 |
如图,小亮同学在晚上由路灯A走向路灯B,当他走到点P时,发现他的身影顶部正好接触路灯B的底部,这时他离路灯A 25米,离路灯B 5米,如果小亮的身高为1.6米,那么路灯高度为 ( )
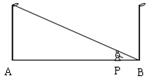
| A.6.4米 | B.8米 | C.9.6米 | D.11.2米 |


