题目内容
【题目】如图,在平面直角坐标系中,A、B均在边长为1的正方形网格格点上.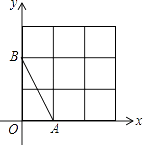
(1)在网格的格点中,找一点C,使△ABC是直角三角形,且三边长均为无理数(只画出一个,并涂上阴影);
(2)若点P在图中所给网格中的格点上,△APB是等腰三角形,满足条件的点P共有个;
(3)若将线段AB绕点A顺时针旋转90°,写出旋转后点B的坐标 .
【答案】
(1)解:直角△ABC如图所示

(2)4
(3)(3,1)
【解析】解:(2)如图, 
点P共有4个;(3)点B的对应点的坐标为(3,1).(3)旋转后的点B如图中B'所示:

所以答案是:4,(3,1).
【考点精析】通过灵活运用等腰三角形的判定和勾股定理的概念,掌握如果一个三角形有两个角相等,那么这两个角所对的边也相等(简称:等角对等边).这个判定定理常用于证明同一个三角形中的边相等;直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2即可以解答此题.

练习册系列答案
相关题目

