题目内容
对于某一自变量为x的函数,若当x=x0时,其函数值也为x0,则称点(x0,x0)为此函数的不动点.现有函数y=
,
(1)若y=
有不动点(4,4),(-4,-4),求a,b;
(2)若函数y=
的图象上有两个关于原点对称的不动点,求实数a,b应满足的条件;
(3)已知a=4时,函数y=
仍有两个关于原点对称的不动点,则此时函数y=
的图象与函数y=-
的图象有什么关系?与函数y=-
的图象又有什么关系?
| 3x+a |
| x+b |
(1)若y=
| 3x+a |
| x+b |
(2)若函数y=
| 3x+a |
| x+b |
(3)已知a=4时,函数y=
| 3x+a |
| x+b |
| 3x+a |
| x+b |
| 5 |
| x+3 |
| 5 |
| x |
(1)将(4,4)、(-4,-4)代入y=
中,得
,解得
(2)令
=x,得:3x+a=x2+bx(x≠-b)
即x2+(b-3)x-a=0
设方程的两根为x1,x2,则两个不动点(x1,x2),(x2,x2),
由于它们关于原点可以得到对称为,所以x1+x2=0,
∴
,解得
,
又因为x≠-b,即x≠-3,所以以a≠9,
因此a,b满足条件a>0且a≠9,b=3;
(3)由(2)知b=3,此时函数为y=
,
即y=3-
∴函数y=
的图象可由y=-
的图象向上平移3个单位得到,
又函数y=-
的图象可由函数y=-
的图象向左平移3个单位得到,
∴函数y=
的图象可由函数y=-
的图象向左平移3个单位,再向上平移3个单位得到.
| 3x+a |
| x+b |
|
|
(2)令
| 3x+a |
| x+b |
即x2+(b-3)x-a=0
设方程的两根为x1,x2,则两个不动点(x1,x2),(x2,x2),
由于它们关于原点可以得到对称为,所以x1+x2=0,
∴
|
|
又因为x≠-b,即x≠-3,所以以a≠9,
因此a,b满足条件a>0且a≠9,b=3;
(3)由(2)知b=3,此时函数为y=
| 3x+4 |
| x+3 |
即y=3-
| 5 |
| x+3 |
∴函数y=
| 3x+4 |
| x+3 |
| 5 |
| x+3 |
又函数y=-
| 5 |
| x+3 |
| 5 |
| x |
∴函数y=
| 3x+4 |
| x+3 |
| 5 |
| x |

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 ,
, 有不动点(4,4),(-4,-4),求a,b;
有不动点(4,4),(-4,-4),求a,b;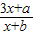 的图象上有两个关于原点对称的不动点,求实数a,b应满足的条件;
的图象上有两个关于原点对称的不动点,求实数a,b应满足的条件; 仍有两个关于原点对称的不动点,则此时函数y=
仍有两个关于原点对称的不动点,则此时函数y= 的图象与函数y=
的图象与函数y= 的图象有什么关系?与函数y=
的图象有什么关系?与函数y= 的图象又有什么关系?
的图象又有什么关系?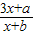 ,
, 有不动点(4,4),(-4,-4),求a,b;
有不动点(4,4),(-4,-4),求a,b; 的图象上有两个关于原点对称的不动点,求实数a,b应满足的条件;
的图象上有两个关于原点对称的不动点,求实数a,b应满足的条件; 仍有两个关于原点对称的不动点,则此时函数y=
仍有两个关于原点对称的不动点,则此时函数y= 的图象与函数y=
的图象与函数y= 的图象有什么关系?与函数y=
的图象有什么关系?与函数y= 的图象又有什么关系?
的图象又有什么关系? ,
,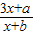 有不动点(4,4),(-4,-4),求a,b;
有不动点(4,4),(-4,-4),求a,b; 的图象上有两个关于原点对称的不动点,求实数a,b应满足的条件;
的图象上有两个关于原点对称的不动点,求实数a,b应满足的条件;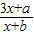 仍有两个关于原点对称的不动点,则此时函数y=
仍有两个关于原点对称的不动点,则此时函数y=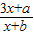 的图象与函数y=
的图象与函数y= 的图象有什么关系?与函数y=
的图象有什么关系?与函数y=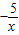 的图象又有什么关系?
的图象又有什么关系?