题目内容
 22、小明不小心敲坏了一块圆形玻璃,于是他拿了其中的一小块到玻璃店去配同样大小的圆形玻璃(如图),店里的师傅说不知圆形玻璃的大小不能配,小明就借了一把尺,先量得其中的一条弦AB的长度为60厘米,然后再量得这个弓形高CD的长度为10厘米,由此就可求得半径解决问题,请你帮小明算一下这个圆的半径是多少厘米.
22、小明不小心敲坏了一块圆形玻璃,于是他拿了其中的一小块到玻璃店去配同样大小的圆形玻璃(如图),店里的师傅说不知圆形玻璃的大小不能配,小明就借了一把尺,先量得其中的一条弦AB的长度为60厘米,然后再量得这个弓形高CD的长度为10厘米,由此就可求得半径解决问题,请你帮小明算一下这个圆的半径是多少厘米.分析:根据题意,已知弦AB的长60,AD=30,CD=10,根据勾股定理和垂径定理可以求得圆的半径.
解答: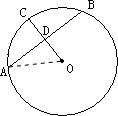 解:设此圆的圆心为点O,半径为r厘米,
解:设此圆的圆心为点O,半径为r厘米,
连接DO、AO、则点C、D、O在一直线上、可得OD=(r-10)cm,
由题意知,得AD=30厘米,
∴r2=302+(r-10)2,
解得r=50,
答:这个圆的半径是50厘米.
 解:设此圆的圆心为点O,半径为r厘米,
解:设此圆的圆心为点O,半径为r厘米,连接DO、AO、则点C、D、O在一直线上、可得OD=(r-10)cm,
由题意知,得AD=30厘米,
∴r2=302+(r-10)2,
解得r=50,
答:这个圆的半径是50厘米.
点评:解决与弦有关的问题时,往往需构造以半径、弦心距和弦长的一半为三边的直角三角形,若设圆的半径为r,弦长为a,这条弦的弦心距为d,则有等式r2=d2+($frac{a}{2}$)2成立,知道这三个量中的任意两个,就可以求出另外一个.

练习册系列答案
 优学名师名题系列答案
优学名师名题系列答案
相关题目
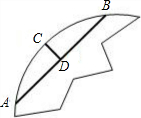 小明不小心敲坏了一块圆形玻璃,于是他拿了其中的一小块到玻璃店去配同样大小的圆形玻璃(如图),店里的师傅说不知圆形玻璃的大小不能配,小明就借了一把尺,先量得其中的一条弦AB的长度为60厘米,然后再量得这个弓形高CD的长度为10厘米,由此就可求得半径解决问题,请你帮小明算一下这个圆的半径是多少厘米.
小明不小心敲坏了一块圆形玻璃,于是他拿了其中的一小块到玻璃店去配同样大小的圆形玻璃(如图),店里的师傅说不知圆形玻璃的大小不能配,小明就借了一把尺,先量得其中的一条弦AB的长度为60厘米,然后再量得这个弓形高CD的长度为10厘米,由此就可求得半径解决问题,请你帮小明算一下这个圆的半径是多少厘米.