题目内容
【题目】(10分)已知△ABC是等边三角形,点D是直线BC上一点,以AD为一边在AD的右侧作等边△ADE.
(1)如图①,点D在线段BC上移动时,直接写出∠BAD和∠CAE的大小关系;
(2)如图②,点D在线段BC的延长线上移动时,猜想∠DCE的大小是否发生变化.若不变请求出其大小;若变化,请说明理由.

【答案】(1)∠BAD=∠CAE;(2)∠DCE=60°,不发生变化.
【解析】试题分析:(1)由等边三角形的性质得出∠BAC=∠DAE,容易得出结论;
(2)由△ABC和△ADE是等边三角形可以得出AB=BC=AC,AD=AE,∠ABC=∠ACB=∠BAC=∠DAE=60°,得出∠ABD=120°,再证明△ABD≌△ACE,得出∠ABD=∠ACE=120°,即可得出结论;
解:(1)∠BAD=∠CAE;理由:
∵△ABC和△ADE是等边三角形,
∴∠BAC=∠DAE=60°,
∴∠BAD=∠CAE;
(2)∠DCE=60°,不发生变化;理由如下:
∵△ABC是等边三角形,△ADE是等边三角形,
∴∠DAE=∠BAC=∠ABC=∠ACB=60°,AB=AC,AD=AE.
∴∠ABD=120°,∠BAC﹣∠BAE=∠DAE﹣∠BAE
∴∠DAB=∠CAE.
在△ABD和△ACE中,
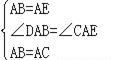 ,
,
∴△ABD≌△ACE(SAS),
∴∠ACE=∠ABD=120°.
∴∠DCE=∠ACE﹣∠ACB=120°﹣60°=60°.
点睛:本题考查了全等三角形的判定与性质以及等边三角形的性质;熟练掌握等边三角形的性质,证明三角形全等是解决问题的关键.

练习册系列答案
相关题目