题目内容
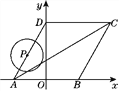
【题目】如图，
的顶点A（0,3），B（b，0），C（c，0）在x轴上，若
。
（1）请判断的形状并予以证明；
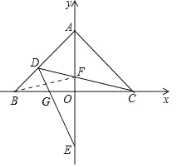
（2）如图，过AB上一点D作射线交y轴负半轴与点E，连CD交y轴与F点。若BD=FD，求
度数。
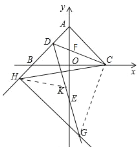
（3）在（2）的条件下，
，H是AB延长线上一动点，作
，HG交射线DE于点G点，则
的值是否变化？若变化，请说明理由；若不变，请求出该值。
【答案】（1）△ABC为等腰直角三角形，理由见解析；（2）15°；（2）2.
【解析】
（1）结论：△ABC是等腰直角三角形．通过
计算出B、C的坐标，结合A的坐标可证明△AOB和△AOC都是等腰直角三角形，继而可证△ABC是等腰直角三角形；
（2）连接BF，分别根据DB=DF， FB=FC可证明∠DBF=∠DFB，∠FBC=∠BCD.根据∠DFB=∠FBC+∠BCD，可设∠FBC=∠BCD=x，利用方程思想求得
度数.
（3）结论：
的值是定值，定值为2．连接CG．在DG上截取DK，使得DK=DH．只要证明DG=DH+CD，CD=2AD即可解决问题.
（1）结论：△ABC是等腰直角三角形.
理由：
∵，
∴b=-3，c=3
∴B（-3，0），C（3，0）
∵A（0，3）
∴OB=OC=OA，
∵AO⊥BC
∴AB=AC，△AOB和△AOC都是等腰直角三角形
∴∠BAO=∠OBA=∠OAC=∠OCA=45°
∴∠BAC=90°
∴△ABC是等腰直角三角形.
（2）证明：如图，连接BF，BE.
∵DB=DF，
∴∠DBF=∠DFB，
∴OA垂直平分线段BC，
∴FB=FC，
∴∠FBC=∠BCD，设∠FBC=∠BCD=x，
∴∠DFB=∠FBC+∠BCD=2x，
∴∠DBF=2x，
∵∠DBF+∠FBC=∠ABO
∴3x=45°，
∴x=15°，
∴∠BCD=15°
（3）结论：
的值是定值，定值为2.
理由：如图2中，连接CG.在DG上截取DK，使得DK=DH.
∵
∴∠AFD=∠OFC=90°-∠BCD=90°-15°=75°
∴∠CDG=∠AFD-∠DEF=75°-15°=60°.
在△BCD中，∠ABC+∠BCD+∠BDC=180°
∴∠BDC=180°-∠ABC-∠BCD=180°-45°-15°=120°
∴∠CDG=∠GDH=60°
∵∠CHG=60°，
∴∠CDG=∠CHG，
∴C，D，H，G四点共圆，
∴∠HCG=∠GDH=60°，
∴△HCG是等边三角形，
∵DH=DK,∠HDK=60°，
∴△HDK是等边三角形，
∵∠DHK=∠CHG=60°，
∴∠DHC=∠KHG，
∵DH=DK，HC=HG，
∴△DHC≌△KHG(SAS)，
∴CD=KG，
∴DG=DK+KG，
∵DK=DH，KG=CD，
∴DG=DH+CD，
∴DGDH=CD，
在Rt△ADC中,∵∠ACD=∠ACB-∠BCD=30°，
∴CD=2AD，
∴DGDH=2AD，
∴.
