题目内容
(2013•邵阳)在△ABC中,若|sinA-
|+(cosB-
)2=0,则∠C的度数是( )
| 1 |
| 2 |
| 1 |
| 2 |
分析:根据绝对值及完全平方的非负性,可求出sinA、cosB的值,继而得出∠A、∠B的度数,利用三角形的内角和定理,可求出∠C的度数.
解答:解:∵|sinA-
|+(cosB-
)2=0,
∴sinA=
,cosB=
,
∴∠A=30°,∠B=60°,
则∠C=180°-30°-60°=90°.
故选D.
| 1 |
| 2 |
| 1 |
| 2 |
∴sinA=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠A=30°,∠B=60°,
则∠C=180°-30°-60°=90°.
故选D.
点评:本题考查了特殊角的三角函数值,三角形的内角和定理,属于基础题,一些特殊角的三角函数值是需要我们熟练记忆的内容.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
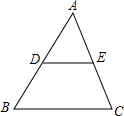 (2013•邵阳)如图所示,在△ABC中,点D、E分别是AB、AC的中点,连结DE,若DE=5,则BC=
(2013•邵阳)如图所示,在△ABC中,点D、E分别是AB、AC的中点,连结DE,若DE=5,则BC=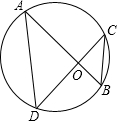 (2013•邵阳)如图所示,弦AB、CD相交于点O,连结AD、BC,在不添加辅助线的情况下,请在图中找出一对相等的角,它们是
(2013•邵阳)如图所示,弦AB、CD相交于点O,连结AD、BC,在不添加辅助线的情况下,请在图中找出一对相等的角,它们是