题目内容
如图在![]() 中,
中,![]() ,
,![]() ,
, ![]() 厘米,点P从点A出发沿线路AB—BC作匀速运动,点
厘米,点P从点A出发沿线路AB—BC作匀速运动,点![]() 从AC的中点D同时出发沿线路DC—CB作匀速运动逐步靠近点P, 设P,Q两点运动的速度分别为1厘米/秒、
从AC的中点D同时出发沿线路DC—CB作匀速运动逐步靠近点P, 设P,Q两点运动的速度分别为1厘米/秒、![]() 厘米/秒(
厘米/秒(![]() ),它们在秒后于BC边上的某一点相遇.
),它们在秒后于BC边上的某一点相遇.
(1) 求出AC与BC的长度.
(2) 试问两点相遇时所在的E点会是BC的中点吗?为什么?
(3) 若以D,E,C为顶点的三角形与![]() 相似,试分别求出
相似,试分别求出![]() 与的值.(精确到0.1)
与的值.(精确到0.1)
 |
解: (1)解法1: 在![]() 中,
中, ![]() ,
,![]() ,
,![]() 厘米,
厘米,
∴![]() (厘米),
(厘米), ![]() (厘米)
(厘米)
解法2: 在![]() 中,
中, ![]() ,
,![]() ,
,![]() 厘米,
厘米,
∴![]() (厘米)
(厘米)
![]() (厘米)
(厘米)
 (2) 解法1:
(2) 解法1:
在秒后,点![]() 运动的路程为
运动的路程为![]() , 点P运动的路程为,那么,
, 点P运动的路程为,那么,
![]() ,
,![]() ,
,
∵![]() ,∴
,∴![]()
所以![]() 点不会是
点不会是![]() 的中点.
的中点.
解法2:
∵![]() , 则
, 则![]()
又![]() (厘米),
(厘米),![]() 厘米,
厘米,
∴![]() ,从而
,从而![]() ,即
,即![]() 点不可能是
点不可能是![]() 的中点
的中点
(3)若以![]() 为顶点的三角形与
为顶点的三角形与![]() 相似,
相似,
当过![]() 点作
点作![]() ,交
,交![]() 于
于![]() ,则△DCE1∽△ACB时,
,则△DCE1∽△ACB时,![]()
∴![]() 点是
点是![]() 的中点
的中点
但![]() ,
,![]() ,∵
,∵![]() ,故
,故![]()
即![]() ,与
,与![]() 点是
点是![]() 的中点矛盾.
的中点矛盾.
当过![]() 点作
点作![]() ,交
,交![]() 于
于![]() ,则△DCE2∽△ABC时,
,则△DCE2∽△ABC时,![]() , 所以,
, 所以,![]()
依题意得,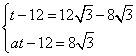 , 解得
, 解得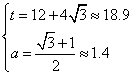 ,
,
所以![]() 秒,
秒, ![]() 厘米/秒
厘米/秒
解法2:
作![]() ,交
,交![]() 于
于![]() ,则 △DCE1∽△ACB
,则 △DCE1∽△ACB
∵![]() ,∴
,∴![]() ,
,
但由(2)可知,![]() ,故这种情况不可能
,故这种情况不可能
又作![]() ,交
,交![]() 于
于![]()
∵![]() ,
,![]() ,
,
∴△DCE2∽△ABC ![]() 即
即![]() ,解得
,解得![]() (厘米)
(厘米)
∴![]() (厘米), 此时
(厘米), 此时![]() 适合题意
适合题意
∴![]() (秒),
(秒),
![]() (厘米/秒 )
(厘米/秒 )

练习册系列答案
相关题目
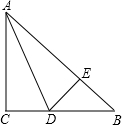 如图在△ABC中,AC=BC,∠C=90°,AD是△ABC的角平分线,DE⊥AB,垂足为E,CD=4cm.求AC的长是多少厘米.
如图在△ABC中,AC=BC,∠C=90°,AD是△ABC的角平分线,DE⊥AB,垂足为E,CD=4cm.求AC的长是多少厘米. (1998•四川)已知:如图⊙O中,CD为直径,半径OA⊥CD,点B在OA上,延长CB交⊙O于点M,
(1998•四川)已知:如图⊙O中,CD为直径,半径OA⊥CD,点B在OA上,延长CB交⊙O于点M,