题目内容
如图,在梯形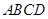 中,
中,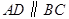 ,
, ,
,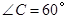 ,
,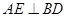 于点E,F是CD的中点,DG是梯形
于点E,F是CD的中点,DG是梯形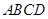 的高.
的高.
(1)求证:四边形AEFD是平行四边形;
(2)设 ,四边形DEGF的面积为y,求y关于x的函数关系式.
,四边形DEGF的面积为y,求y关于x的函数关系式.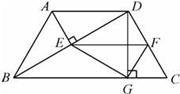
(1) 证明: ∵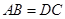 ,∴梯形ABCD为等腰梯形.
,∴梯形ABCD为等腰梯形.
∵∠C=60°,∴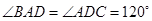 .
.
又∵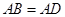 ,∴
,∴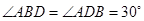 .
.
∴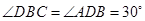 .∴
.∴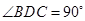 .
.
由已知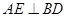 ,∴AE∥DC.
,∴AE∥DC.
又∵AE为等腰三角形ABD的高, ∴E是BD的中点,
∵F是DC的中点, ∴EF∥BC. ∴EF∥AD.
∴四边形AEFD是平行四边形.
(2)解:在Rt△AED中, 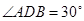 ,∵
,∵ ,∴
,∴ .
.
在Rt△DGC中 ∠C=60°,并且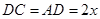 ,∴
,∴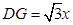 .
.
由(1)知: 在平行四边形AEFD中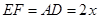 ,又∵
,又∵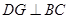 ,∴
,∴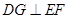 ,
,
∴四边形DEGF的面积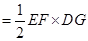 ,
,
∴ 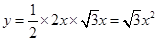
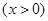 .
.
解析

练习册系列答案
相关题目
 如图,在梯形中ABCD中,AD∥BC,∠ABC=90°,BE⊥CD于点E,AB=BE.
如图,在梯形中ABCD中,AD∥BC,∠ABC=90°,BE⊥CD于点E,AB=BE.
 中,
中, ,
, ,
, ,
, ,
, 为
为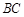 上一动点,则
上一动点,则 周长的最小值为 .
周长的最小值为 .
 中,
中, ∥
∥ ,
, ,
, ,点
,点 在对角线
在对角线 上,作
上,作 ,连接
,连接 ,且满足
,且满足 .
.
 ;
; 时,试判断四边形
时,试判断四边形 的形状,并说明理由.
的形状,并说明理由. 中,
中, 两点在边
两点在边 上,且四边形
上,且四边形 是平行四边形.
是平行四边形.
 与
与 时,求证:平行四边形
时,求证:平行四边形