题目内容
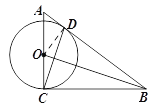
【题目】如图,在△ABC中,∠ ACB=90°,点D在BC边上,且BD=BC,过点B作CD的垂线交AC于点O,以O为圆心,OC为半径画圆.
(1)求证:AB是⊙O的切线;
(2)若AB=10,AD=2,求⊙O的半径.
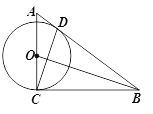
【答案】(1)证明见解析;(2)⊙O的半径为![]()
【解析】(1)连接OD,先证△DBO≌△CBO,再证∠ODB=∠OCB=90°即可;(2)在Rt△ABC中由勾股定理建立方程,从而求出⊙O的半径.
(1)证明:连接OD
∵BD=BC,BO⊥CD
∴∠DBO=∠CBO
∵BD=BC,∠DBO=∠CBO,OB=OB
∴△DBO≌△CBO
∴OD=OC,∠ODB=∠OCB=90°
∴AB是⊙O的切线
(2)∵AB=10,AD=2,∴BC=BD=AB-AD=8
在Rt△ABC中, ![]()
设⊙O的半径为r,则OD=OC=r,AO=AC-OC=6-r
在Rt△ADO中,∵AD2+OD2=AO2
∴22+r 2=(6-r)2
解之得![]() ,即⊙O的半径为
,即⊙O的半径为![]()
“点睛”本题考查了圆的切线的判定以及勾股定理的运用,解题关键是在直角三角形中利用勾股定理列出方程.

练习册系列答案
相关题目