题目内容
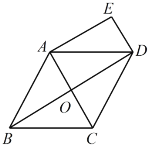
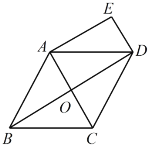
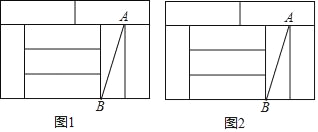
【题目】如图,在△ABC和△ADE中,AB=AD,AC=AE,∠1=∠2

(1)求证:△ABC≌△ADE;
(2)找出图中与∠1、∠2相等的角(直接写出结论,不需证明).
【答案】(1)证明见解析;(2)∠MFD和∠NFC,理由见解析.
【解析】
(1)根据等式性质可以得出∠BAC=∠DAE,进而运用SAS判定△ABC≌△ADE; (2)根据全等三角形的对应角相等,可以发现∠B=∠D,∠E=∠C,进而得出与∠1、∠2相等的角有∠MFD和∠NFC.
本题解析:
(1)证明:∵∠1=∠2,
∴∠1+∠MAC=∠2+∠NAC,
∴∠BAC=∠DAE,
在△ABC和△ADE中,
 ,
,
∴△ABC≌△ADE(SAS);
(2)图中与∠1、∠2相等的角有∠MFD和∠NFC.


练习册系列答案
相关题目
【题目】(本小题满分10分)小红的妈妈开了间海产品干货店,今年从沿海地区进了一批墨鱼干,以60元/千克的价格销售,由于墨鱼干质量好,价格便宜,加上来旅游的顾客很多,一时间销售了不少.妈妈看到生意红火,决定经过提价来增加利润.于是先后将售价提高到80元/千克和100元/千克,销售量依次减少了,但每天的利润依次增加,然后她又把售价调到140元/千克,此时过往的顾客大多数嫌贵,销售量明显下降,连利润也呈下降趋势.面对如此情况,小红思考了一个问题:售价究竟定为多少才使每天的利润最大呢?
小红看了妈妈的账单后马上进行了分析调查,从账单上了解到如下数据:
售价(元/千克) | 60 | 80 | 100 | 120 | 140 |
每天销售量(千克) | 22.5 | 20 | 17.5 | 15 | 12.5 |
请你利用数学知识帮小红计算一下,
(1)设销售量为y千克,售价为x元,y与x之间的关系式.
(2)售价究竟定为多少元才能每天的销售额最大. (销售额=售价![]() 销售量)
销售量)