题目内容
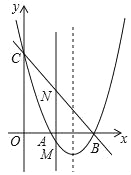
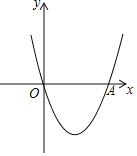
【题目】如图,己知点A是双曲线y=kx-1(k>0)上的一个动点,连AO并延长交另一分支于点B,以AB为边作等边△ABC,点C在第四象限.随着点A的运动,点C的位置也不断变化,但点C始终在双曲线y=mx-1(m<0)上运动,则m与k的关系是( )

A. m= -kB. m=![]() kC. m= -2kD. m= -3k
kC. m= -2kD. m= -3k
【答案】D
【解析】
设点A的坐标为(a,![]() ),连接OC,则OC⊥AB,表示出OC,过点C作CD⊥x轴于点D,设出点C坐标,在Rt△OCD中,利用勾股定理可得出x2的值,进而得出结论.
),连接OC,则OC⊥AB,表示出OC,过点C作CD⊥x轴于点D,设出点C坐标,在Rt△OCD中,利用勾股定理可得出x2的值,进而得出结论.
如图,
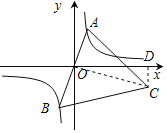
设A(a,![]() ),
),
∵点A与点B关于原点对称,
∴OA=OB,
∵△ABC为等边三角形,
∴AB⊥OC,OC=![]() AO,
AO,
∵AO=![]()
∴CO=![]() ,
,
过点C作CD⊥x轴于点D,
则可得∠AOD=∠OCD(都是∠COD的余角),
设点C的坐标为(x,y),则tan∠AOD=tan∠OCD,即![]()
解得y=-![]() .
.
在Rt△COD中,CD2+OD2=OC2,即y2+x2=3a2+![]() ,将y=-
,将y=-![]() 代入得,x2=
代入得,x2=![]() ,
,
∴x=![]() ,y=-
,y=-![]() =-
=-![]() ,
,
∴m=xy=![]() =-3k.
=-3k.
故选D.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】已知y是x的函数,自变量x的取值范围是x>0,下表是y与x的几组对应值.
x | … | 1 | 2 | 4 | 5 | 6 | 8 | 9 | … |
y | … | 3.92 | 1.95 | 0.98 | 0.78 | 2.44 | 2.44 | 0.78 | … |
小风根据学习函数的经验,利用上述表格所反映出的y与x之间的变化规律,对该函数的图象和性质进行了探究.
下面是小风的探究过程,请补充完整:
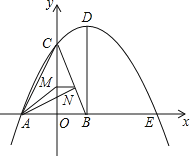
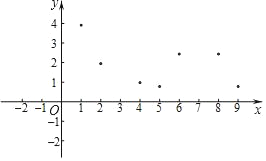
(1)如图,在平面直角坐标系xOy中,描出了以上表中各对对应值为坐标的点.根据描出的点,画出该函数的图象;
(2)根据画出的函数图象,写出:
①x=7对应的函数值y约为多少;
②写出该函数的一条性质.
【题目】某服装厂每天生产![]() 、
、![]() 两种品牌的服装共600件,
两种品牌的服装共600件,![]() 、
、![]() 两种品牌的服装每件的成本和利润如右表:
两种品牌的服装每件的成本和利润如右表:
A | B | |
成本(元/件) | 50 | 35 |
利润(元/件) | 20 | 15 |
设每天生产![]() 种品牌服装
种品牌服装![]() 件,每天两种服装获利
件,每天两种服装获利![]() 元.
元.
(1)请写出![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(2)如果服装厂每天至少投入成本26400元,那么每天至少获利多少元?