题目内容
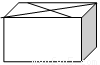
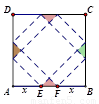
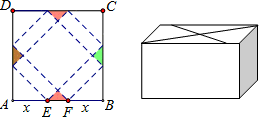 一个包装盒的设计方法如图所示,ABCD是边长为60cm的正方形硬纸片,切去阴影部分所示的四个全等的等腰直角三角形,再沿虚线折起,使得ABCD四个点重合于图中的点P,正好形成一个正四棱柱形状的包装盒,E、F在AB上是被切去的等腰直角三角形斜边的两个端点,设AE=FB=xcm.若广告商要求包装盒侧面积S(cm2)最大,试问x应取的值为________cm.
一个包装盒的设计方法如图所示,ABCD是边长为60cm的正方形硬纸片,切去阴影部分所示的四个全等的等腰直角三角形,再沿虚线折起,使得ABCD四个点重合于图中的点P,正好形成一个正四棱柱形状的包装盒,E、F在AB上是被切去的等腰直角三角形斜边的两个端点,设AE=FB=xcm.若广告商要求包装盒侧面积S(cm2)最大,试问x应取的值为________cm.
15
分析:可设包装盒的高为h(cm),底面边长为a(cm),写出a,h与x的关系式,并注明x的取值范围.再利用侧面积公式表示出包装盒侧面积S关于x的函数解析式,最后求出何时它取得最大值即可;
解答:设包装盒的高为h(cm),底面边长为a(cm),则a= x,h=
x,h= (30-x),0<x<30.
(30-x),0<x<30.
S=4ah=8x(30-x)=-8(x-15)2+1800,
∴当x=15cm时,S取最大值.
故答案为:15.
点评:考查函二次函数的最值、等腰直角三角形及正方形的性质,同时还考查了考查运算求解能力、空间想象能力、数学建模能力.属于基础题.
分析:可设包装盒的高为h(cm),底面边长为a(cm),写出a,h与x的关系式,并注明x的取值范围.再利用侧面积公式表示出包装盒侧面积S关于x的函数解析式,最后求出何时它取得最大值即可;
解答:设包装盒的高为h(cm),底面边长为a(cm),则a=
 x,h=
x,h= (30-x),0<x<30.
(30-x),0<x<30.S=4ah=8x(30-x)=-8(x-15)2+1800,
∴当x=15cm时,S取最大值.
故答案为:15.
点评:考查函二次函数的最值、等腰直角三角形及正方形的性质,同时还考查了考查运算求解能力、空间想象能力、数学建模能力.属于基础题.

练习册系列答案
相关题目
 (2013•泰州一模)一个包装盒的设计方法如图所示,ABCD是边长为60cm的正方形硬纸片,切去阴影部分所示的四个全等的等腰直角三角形,再沿虚线折起,使得ABCD四个点重合于图中的点P,正好形成一个正四棱柱形状的包装盒,E、F在AB上是被切去的等腰直角三角形斜边的两个端点,设AE=FB=xcm.若广告商要求包装盒侧面积S(cm2)最大,试问x应取的值为
(2013•泰州一模)一个包装盒的设计方法如图所示,ABCD是边长为60cm的正方形硬纸片,切去阴影部分所示的四个全等的等腰直角三角形,再沿虚线折起,使得ABCD四个点重合于图中的点P,正好形成一个正四棱柱形状的包装盒,E、F在AB上是被切去的等腰直角三角形斜边的两个端点,设AE=FB=xcm.若广告商要求包装盒侧面积S(cm2)最大,试问x应取的值为


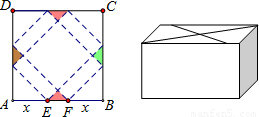
 四个点重合于图中的点P,正好形成一个正四棱柱形状的包装盒,E、F在AB上是被切去的等腰直角三角形斜边的两个端点,设AE = FB = xcm。若广告商要求包装盒侧面积S(cm
四个点重合于图中的点P,正好形成一个正四棱柱形状的包装盒,E、F在AB上是被切去的等腰直角三角形斜边的两个端点,设AE = FB = xcm。若广告商要求包装盒侧面积S(cm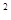 )大,试问x应取的值为
cm.
)大,试问x应取的值为
cm.