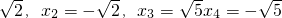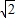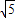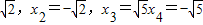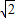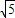Question

阅读材料：为了解方程（x²-1）²-5（x²-1）+4=0，我们可以将x²-1视为一个整体，然后设x²-1=y，（x²-1）²=y²，
则原方程可化为y²-5y+4=0①
解得y₁=1，y₂=4．
当y=1时，x²-1=1，x²=2，∴x=±

2

当y=4时，x²-1=4，x²=5，∴x=±

5

∴原方程的解为：x₁=

2

，x2=-

2

，x3=

5

x4=-

5

解答问题：仿造上题解方程：x⁴-6x²+8=0．

Answer 1

设x²=y，x⁴=y²，则原方程可化为y²-6y+8=0，
解得y₁=2，y₂=4．
当y=2时，x2=2，x=±

2

，
当y=4时，x²=4，x=±2．
∴原方程的解为：x1=

2

，x2=-

2

，x3=2，x4=-2．