题目内容
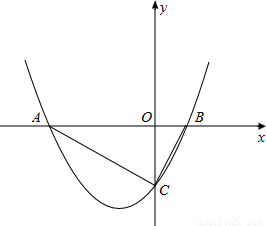
(2010•常德)如图,已知抛物线y= x2+bx+c与x轴交于点A(-4,0)和B(1,0)两点,与y轴交于C点.
x2+bx+c与x轴交于点A(-4,0)和B(1,0)两点,与y轴交于C点.(1)求此抛物线的解析式;
(2)设E是线段AB上的动点,作EF∥AC交BC于F,连接CE,当△CEF的面积是△BEF面积的2倍时,求E点的坐标;
(3)若P为抛物线上A、C两点间的一个动点,过P作y轴的平行线,交AC于Q,当P点运动到什么位置时,线段PQ的值最大,并求此时P点的坐标.
【答案】分析:(1)将A、B的坐标代入抛物线的解析式中,即可求出待定系数的值;
(2)根据抛物线的解析式可得出C点的坐标,易证得△ABC是直角三角形,则EF⊥BC;△CEF和△BEF同高,则面积比等于底边比,由此可得出CF=2BF;易证得△BEF∽△BAC,根据相似三角形的性质,即可求得BE、AB的比例关系,由此可求出E点坐标;
(3)PQ的长实际是直线AC与抛物线的函数值的差,可设P点横坐标为m,用m表示出P、Q的纵坐标,然后可得出PQ的长与m的函数关系式,根据所得函数的性质即可求出PQ最大时,m的值,也就能求出此时P点的坐标.
解答: 解:(1)由题意,得:
解:(1)由题意,得: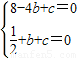 ,
,
解得 ;
;
∴y= x2+
x2+ x-2;
x-2;
(2)由(1)知:C(0,-2);
则AC2=AO2+OC2=20,BC2=BO2+OC2=5;
而AB2=25=AC2+BC2;
∴△ACB是直角三角形,且∠ACB=90°;
∵EF∥AC,
∴EF⊥BC;
∵S△CEF=2S△BEF,
∴CF=2BF,BC=3BF;
∵EF∥AC,
∴ ;
;
∵AB=5,
∴BE= ;
;
OE=BE-OB= ,故E(
,故E( ,0);
,0);
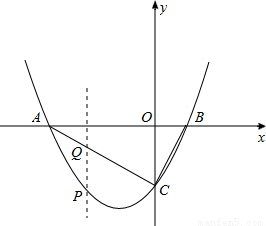
(3)设P点坐标为(m, m2+
m2+ m-2);
m-2);
已知A(-4,0),C(0,-2),
设直线AC的解析式为:
y=kx-2,
则有:-4k-2=0,k=- ;
;
∴直线AC的解析式为y=- x-2;
x-2;
∴Q点坐标为(m,- m-2);
m-2);
则PQ=- m-2-(
m-2-( m2+
m2+ m-2)=-
m-2)=- m2-2m;
m2-2m;
∴当m=-2,即P(-2,-3)时,PQ最大,且最大值为2.
故当P运动到OA垂直平分线上时,PQ的值最大,此时P(-2,-3).
点评:此题考查了二次函数解析式的确定、直角三角形的判定和性质、三角形面积的求法、相似三角形的判定和性质、二次函数的应用等知识,综合性强,难度较大.
(2)根据抛物线的解析式可得出C点的坐标,易证得△ABC是直角三角形,则EF⊥BC;△CEF和△BEF同高,则面积比等于底边比,由此可得出CF=2BF;易证得△BEF∽△BAC,根据相似三角形的性质,即可求得BE、AB的比例关系,由此可求出E点坐标;
(3)PQ的长实际是直线AC与抛物线的函数值的差,可设P点横坐标为m,用m表示出P、Q的纵坐标,然后可得出PQ的长与m的函数关系式,根据所得函数的性质即可求出PQ最大时,m的值,也就能求出此时P点的坐标.
解答:
 解:(1)由题意,得:
解:(1)由题意,得: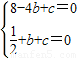 ,
,解得
 ;
;∴y=
 x2+
x2+ x-2;
x-2;(2)由(1)知:C(0,-2);
则AC2=AO2+OC2=20,BC2=BO2+OC2=5;
而AB2=25=AC2+BC2;
∴△ACB是直角三角形,且∠ACB=90°;
∵EF∥AC,
∴EF⊥BC;
∵S△CEF=2S△BEF,
∴CF=2BF,BC=3BF;
∵EF∥AC,
∴
 ;
;∵AB=5,
∴BE=
 ;
;OE=BE-OB=
 ,故E(
,故E( ,0);
,0);
(3)设P点坐标为(m,
 m2+
m2+ m-2);
m-2);已知A(-4,0),C(0,-2),
设直线AC的解析式为:
y=kx-2,
则有:-4k-2=0,k=-
 ;
;∴直线AC的解析式为y=-
 x-2;
x-2;∴Q点坐标为(m,-
 m-2);
m-2);则PQ=-
 m-2-(
m-2-( m2+
m2+ m-2)=-
m-2)=- m2-2m;
m2-2m;∴当m=-2,即P(-2,-3)时,PQ最大,且最大值为2.
故当P运动到OA垂直平分线上时,PQ的值最大,此时P(-2,-3).
点评:此题考查了二次函数解析式的确定、直角三角形的判定和性质、三角形面积的求法、相似三角形的判定和性质、二次函数的应用等知识,综合性强,难度较大.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
 x2+bx+c与x轴交于点A(-4,0)和B(1,0)两点,与y轴交于C点.
x2+bx+c与x轴交于点A(-4,0)和B(1,0)两点,与y轴交于C点.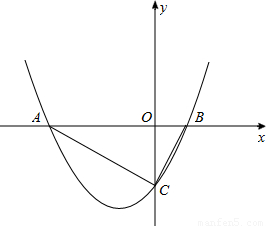
 时,求CH的长.
时,求CH的长.

 时,求CH的长.
时,求CH的长.