题目内容
【题目】学校需要购买一批篮球和足球,已知一个篮球比一个足球的进价高30元,买两个篮球和三个足球一共需要510元.
(1)求篮球和足球的单价;
(2)根据实际需要,学校决定购买篮球和足球共100个,其中篮球购买的数量不少于足球数量的![]() ,学校可用于购买这批篮球和足球的资金最多为10500元.请问有几种购买方案?
,学校可用于购买这批篮球和足球的资金最多为10500元.请问有几种购买方案?
(3)若购买篮球x个,学校购买这批篮球和足球的总费用为y(元),在(2)的条件下,求哪种方案能使y最小,并求出y的最小值.
【答案】(1)120,90;(2)11种;(3)购买篮球40,足球60个时,y最小值为10200元.
【解析】
试题分析:(1)设一个篮球x元,则一个足球(x﹣30)元,根据“买两个篮球和三个足球一共需要510元”列出方程,即可解答;
(2)设购买篮球x个,足球(100﹣x)个,根据“篮球购买的数量不少于足球数量的![]() ,学校可用于购买这批篮球和足球的资金最多为10500元”,列出不等式组,求出x的取值范围,由x为正整数,即可解答;
,学校可用于购买这批篮球和足球的资金最多为10500元”,列出不等式组,求出x的取值范围,由x为正整数,即可解答;
(3)表示出总费用y,利用一次函数的性质,即可确定x的取值,即可确定最小值.
试题解析:(1)设一个篮球x元,则一个足球(x﹣30)元,由题意得:2x+3(x﹣30)=510,解得:x=120,∴一个篮球120元,一个足球90元;
(2)设购买篮球x个,足球(100﹣x)个,由题意可得: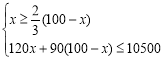 ,解得:40≤x≤50,∵x为正整数,∴x=40,41,42,43,44,45,46,47,48,49,50,∴共有11种购买方案;
,解得:40≤x≤50,∵x为正整数,∴x=40,41,42,43,44,45,46,47,48,49,50,∴共有11种购买方案;
(3)由题意可得y=120x+90(100﹣x)=30x+9000(40≤x≤50),∵k=30>0,∴y随x的增大而增大,∴当x=40时,y有最小值,y最小=30×40+9000=10200(元),所以当x=40时,y最小值为10200元.

 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案