题目内容
下列结论:①不论a为何值
都有意义;②a=-1时,分式
的值为0;③若
的值为负,则x的取值范围是x<1;④若
÷
有意义,则x的取值范围是x≠-2且x≠0.其中正确的是( )
| a |
| a2+1 |
| a+1 |
| a2-1 |
| x2+1 |
| x-1 |
| x+1 |
| x+2 |
| x+1 |
| x |
| A、①②③④ | B、①②③ |
| C、①③ | D、①④ |
分析:根据分式有意义的条件对各式进行逐一分析即可.
解答:解:①正确,∵a不论为何值不论a2+2>0,∴不论a为何值
都有意义;
②错误,∵当a=-1时,a2-1=1-1=0,此时分式无意义,∴此结论错误;
③正确,∵若
的值为负,即x-1<0,即x<1,∴此结论正确;
④错误,根据分式成立的意义及除数不能为0的条件可知,若
÷
有意义,则x的取值范围是即
,x≠-2,x≠0且x≠-1,故此结论错误.
故选C.
| a |
| a2+1 |
②错误,∵当a=-1时,a2-1=1-1=0,此时分式无意义,∴此结论错误;
③正确,∵若
| x2+1 |
| x-1 |
④错误,根据分式成立的意义及除数不能为0的条件可知,若
| x+1 |
| x+2 |
| x+1 |
| x |
|
故选C.
点评:本题考查的是分式有意义的条件,解答此题要注意④中除数不能为0,否则会造成误解.

练习册系列答案
 期末集结号系列答案
期末集结号系列答案
相关题目
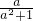 都有意义;②a=-1时,分式
都有意义;②a=-1时,分式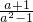 的值为0;③若
的值为0;③若 的值为负,则x的取值范围是x<1;④若
的值为负,则x的取值范围是x<1;④若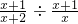 有意义,则x的取值范围是x≠-2且x≠0.其中正确的是
有意义,则x的取值范围是x≠-2且x≠0.其中正确的是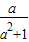 都有意义;②a=-1时,分式
都有意义;②a=-1时,分式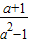 的值为0;③若
的值为0;③若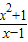 的值为负,则x的取值范围是x<1;④若
的值为负,则x的取值范围是x<1;④若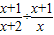 有意义,则x的取值范围是x≠-2且x≠0.其中正确的是( )
有意义,则x的取值范围是x≠-2且x≠0.其中正确的是( )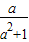 都有意义;②a=-1时,分式
都有意义;②a=-1时,分式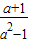 的值为0;③若
的值为0;③若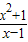 的值为负,则x的取值范围是x<1;④若
的值为负,则x的取值范围是x<1;④若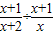 有意义,则x的取值范围是x≠-2且x≠0.其中正确的是( )
有意义,则x的取值范围是x≠-2且x≠0.其中正确的是( )