题目内容
桌面上有大小两颗球,相互靠在一起.已知大球的半径为20cm,小球半径5cm,则这两颗球分别与桌面相接触的两点之间的距离等于分析:首先根据题意作图,可得:⊙A与⊙B外切,⊙A,⊙B与CD分别相切于C,D,AC=20cm,BD=5cm,然后过点B作BE⊥AC,又由切线的性质,即可得四边形ECDB是矩形,则在Rt△AEB中,即可求得BE的长,即可求得这两颗球分别与桌面相接触的两点之间的距离CD的长.
解答:解:如图,根据题意得:⊙A与⊙B外切,⊙A,⊙B与CD分别相切于C,D,AC=20cm,BD=5cm,
∴AB=25cm,AC⊥CD,BD⊥CD,
∴∠ACD=∠BDC=90°,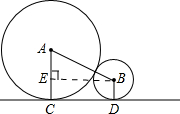
过点B作BE⊥AC,
∴∠BEC=90°,
∴四边形ECDB是矩形,
∴BE=CD,EC=BD=5cm,
∴AE=AC-EC=15cm,
在Rt△AEB中,BE=
=
=20(cm),
∴CD=20cm.
故答案为:20.
∴AB=25cm,AC⊥CD,BD⊥CD,
∴∠ACD=∠BDC=90°,

过点B作BE⊥AC,
∴∠BEC=90°,
∴四边形ECDB是矩形,
∴BE=CD,EC=BD=5cm,
∴AE=AC-EC=15cm,
在Rt△AEB中,BE=
| AB2-AE2 |
| 252-152 |
∴CD=20cm.
故答案为:20.
点评:此题考查了外切两圆的性质,切线的性质,以及矩形的性质等知识.此题综合性较强,难度适中,解题的关键是注意数形结合思想的应用与辅助线的作法.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目