题目内容
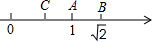 如图所示,数轴上表示1和
如图所示,数轴上表示1和| 2 |
(1)线段长度:AB=
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
(2)设C点表示的数为x,试求|x-
| 2 |
分析:(1)用表示点B的数减去表示点A的数即可;根据对称性,AC=AB;
先表示点C的数,然后用表示点C的数减去表示点0的数即可;
(2)把x代入,然后根据绝对轴的性质进行计算即可得解.
先表示点C的数,然后用表示点C的数减去表示点0的数即可;
(2)把x代入,然后根据绝对轴的性质进行计算即可得解.
解答:解:(1)∵1和
的对应点分别为A、B,
∴AB=
-1;
∵点B关于点A的对称点是C,
∴AC=AB=
-1;
设点C表示的数是x,则1-x=
-1,
解得x=2-
,
∴OC=2-
-0=2-
;
(2)根据(1)可得x=2-
,
∴|x-
|+x=|2-
-
|+2-
=2
-2+2-
=
.
| 2 |
∴AB=
| 2 |
∵点B关于点A的对称点是C,
∴AC=AB=
| 2 |
设点C表示的数是x,则1-x=
| 2 |
解得x=2-
| 2 |
∴OC=2-
| 2 |
| 2 |
(2)根据(1)可得x=2-
| 2 |
∴|x-
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
点评:本题考查了实数与数轴,绝对值以及两点间的距离的求解,求数轴上两点间的距离,用右边的数减去左边的数即可.

练习册系列答案
相关题目
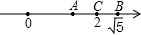 如图所示,数轴上表示2,
如图所示,数轴上表示2,| 5 |
A、-
| ||
B、2-
| ||
C、4-
| ||
D、
|
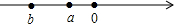 如图所示,数轴上表示a、b两个实数的点的位置,化简|a-b|-
如图所示,数轴上表示a、b两个实数的点的位置,化简|a-b|-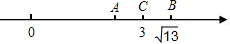 如图所示,数轴上表示3、
如图所示,数轴上表示3、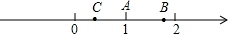 如图所示,数轴上表示1,
如图所示,数轴上表示1,