题目内容
【题目】在平面直角坐标系中，已知一次函数y=﹣ 
x+6与x，y轴分别交于A，B两点，点C（0，n）是y轴上一点，把坐标平面沿直线AC折叠，点B刚好落在x轴上，则点C的坐标是（ ）
A.（0，3）
B.（0， 
）
C.（0， 
）
D.（0， 
）
【答案】C
【解析】解：过C作CD⊥AB于D，如图，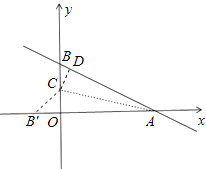 
对于直线y=﹣ 
x+6，
当x=0，得y=6；当y=0，x=8，
∴A（8，0），B（0，6），即OA=8，OB=6，
∴AB=10，
又∵坐标平面沿直线AC折叠，使点B刚好落在x轴上，
∴AC平分∠OAB，
∴CD=CO=n，则BC=6﹣n，
∴DA=OA=8，
∴DB=10﹣8=2，
在Rt△BCD中，DC2+BD2=BC2，
∴n2+22=（6﹣n）2，解得n= 
，
∴点C的坐标为（0， ）．
所以答案是：C．
练习册系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
