题目内容
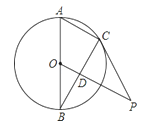
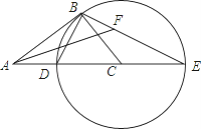
【题目】如图,在Rt△ABC中,∠ABC=90°,以CB为半径作⊙C,交AC于点D,交AC的延长线于点E,连接ED,BE.
(1)求证:△ABD∽△AEB;
(2)当 ![]() =
= ![]() 时,求tanE;
时,求tanE;
(3)在(2)的条件下,作∠BAC的平分线,与BE交于点F,若AF=2,求⊙C的半径.
【答案】(1)证明见解析;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)要证明△ABD∽△AEB,已经有一组对应角是公共角,只需要再找出另一组对应角相等即可;(2)由于AB:BC=4:3,可设AB=4,BC=3,求出AC的值,再利用(1)中结论可得AB2=ADAE,进而求出AE的值,所以tanE=![]() ;(3)设AB=4x,BC=3x,由于已知AF的值,构造直角三角形后利用勾股定理列方程求出x的值,即可知道半径3x的值.
;(3)设AB=4x,BC=3x,由于已知AF的值,构造直角三角形后利用勾股定理列方程求出x的值,即可知道半径3x的值.
(1)证明:∵∠ABC=90°,
∴∠ABD=90°﹣∠DBC,
由题意知:DE是直径,
∴∠DBE=90°,
∴∠E=90°﹣∠BDE,
∵BC=CD,
∴∠DBC=∠BDE,
∴∠ABD=∠E,
∵∠A=∠A,
∴△ABD∽△AEB;
(2)解:∵AB:BC=4:3,
∴设AB=4,BC=3,
∴AC= ![]() =5,
=5,
∵BC=CD=3,
∴AD=AC﹣CD=5﹣3=2,
由(1)可知:△ABD∽△AEB,
∴ ![]() ,
,
∴AB2=ADAE,
∴42=2AE,
∴AE=8,
在Rt△DBE中
tanE= ![]() =
= ![]() =
= ![]()
(3)过点F作FM⊥AE于点M,
∵AB:BC=4:3,
∴设AB=4x,BC=3x,
∴由(2)可知;AE=8x,AD=2x,
∴DE=AE﹣AD=6x,
∵AF平分∠BAC,
∴ ![]() ,
,
∴ ![]() ,
,
∵tanE= ![]() ,
,
∴cosE= ![]() ,sinE=
,sinE= ![]() ,
,
∴ ![]() ,
,
∴BE= ![]() ,
,
∴EF= ![]() BE=
BE= ![]() ,
,
∴sinE= ![]() =
= ![]() ,
,
∴MF= ![]() ,
,
∵tanE= ![]() ,
,
∴ME=2MF= ![]() ,
,
∴AM=AE﹣ME= ![]() ,
,
∵AF2=AM2+MF2 ,
∴4= ![]() +
+ ![]() ,
,
∴x= ![]() ,
,
∴⊙C的半径为:3x= ![]() .
.

 阅读快车系列答案
阅读快车系列答案