题目内容
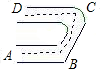
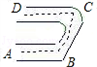
 8、如图一个弯形管道ABCD的拐角∠ABC=120°,∠BCD=60°,这时说管道AB∥CD,是根据
8、如图一个弯形管道ABCD的拐角∠ABC=120°,∠BCD=60°,这时说管道AB∥CD,是根据同旁内角互补,两直线平行
.分析:由已知∠ABC=120°,∠BCD=60°,即∠ABC+∠BCD=120°+60°=180°,可得关于AB∥CD的判定条件:同旁内角互补,两直线平行.
解答:解:∵∠ABC=120°,∠BCD=60°,
∴∠ABC+∠BCD=120°+60°=180°,
∴AB∥CD(同旁内角互补,两直线平行).
∴∠ABC+∠BCD=120°+60°=180°,
∴AB∥CD(同旁内角互补,两直线平行).
点评:本题考查的是平行线的判定,即内错角相等,两直线平行;同位角相等两直线平行;同旁内角互补两直线平行.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图一个弯形管道ABCD的拐角∠ABC=120°,∠BCD=60°,这时说管道AB∥CD,是根据________.
如图一个弯形管道ABCD的拐角∠ABC=120°,∠BCD=60°,这时说管道AB∥CD,是根据________.