Question

【题目】如图，AB⊥OD，∠BOC比∠DOC大34°，OE平分∠AOC，求：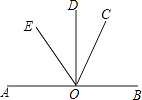

（1）∠COD的大小；
（2）∠DOE的大小．

Answer 1

【答案】
（1）解：由题意可得：设∠DOC=x°，则∠BOC=x°+34°，

∵AB⊥OD，

∴∠DOC+∠BOC=90°，

则x°+x°+34°=90°，

解得：x=28．

故∠COD的度数为28°

（2）解：∵∠AOD=90°，∠DOC=34°，

∴∠AOC=124°，

∵OE平分∠AOC，

∴∠EOC=∠AOE=62°，

∴∠DOE的度数为：∠EOC﹣∠DOC=62°﹣28°=34°

【解析】（1）结合已知设∠DOC=x°，则∠BOC=x°+34°，再利用垂直的定义得出答案；（2）利用（1）中所求，结合角平分线的性质求出答案．