题目内容
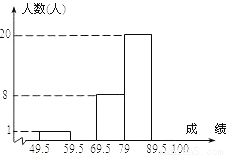
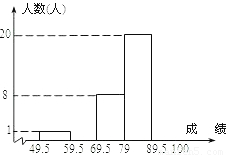
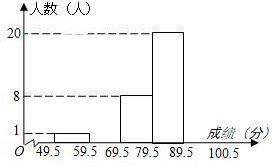
某校为了了解学生对世博礼仪的知晓程度,从全校1200名学生中随机抽取了50名学生进行测试.根据测试成绩(成绩取整数,满分为100分)作了统计分析,绘制成频数分布直方图(如图,其中部分数据缺失).又 知90分以上(含90分)的人数比60~70分(含60分,不含70分)的人数的2倍还多3人.
知90分以上(含90分)的人数比60~70分(含60分,不含70分)的人数的2倍还多3人.
请你根据上述信息,解答下列问题:
(1)该统计分析的样本是(______)
A、1200名学生;
B、被抽取的50名学生;
C、被抽取的50名学生的问卷成绩;
D、50
(2)被测学生中,成绩不低于90分的有多少人?
(3)测试成绩的中位数所在的范围是______;
(4)如果把测试成绩不低于80分记为优良,试估计该校有多少名学生对世博礼仪的知晓程度达到优良;
(5)学校准备从测试成绩不低于90分的学生中随机选3人义务宣传世博礼仪,若小杰的得分是93分,那么小杰被选上的概率是多少?
解:(1)C;
(2)设60~70(分)(含60分,不含70分)的人数为x人,
则90分以上(含90分)的人数为(2x+3)人,
可得3x+3=21,
∴x=6
∴2x+3=15;
(3)79.5-89.5;
(4)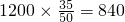 ;
;
(5) .
.
分析:(1)样本就是研究中实际观测或调查的一部分个体称为样本.依据定义即可解答;
(2)设60~70(分)(含60分,不含70分)的人数为x人,则90分以上(含90分)的人数为(2x+3)人,根据60~70(分)(含60分,不含70分)的人数与90分以上(含90分)的人数的和是21人,即可求得x的值,进而求解;
(3)中位数就是把各个数按从小到大的顺序排列排列,中间即第25与第26两个数的平均数,依据定义即可求解;
(4)求出优良的学生所占的比例,即可求得人数;
(5)求出成绩不低于90分的学生的总人数,根据概率公式,即可求解.
点评:本题考查的知识点较多,有样本的概念,中位数的确定方法,频数与频率的关系,对于每个概念的正确理解是解题关键.用到的知识点为:概率=所求情况数与总情况数之比.一组数据按顺序排列后,中间的那两个数的平均数或中间的那个数叫做中位数.
(2)设60~70(分)(含60分,不含70分)的人数为x人,
则90分以上(含90分)的人数为(2x+3)人,
可得3x+3=21,
∴x=6
∴2x+3=15;
(3)79.5-89.5;
(4)
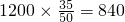 ;
;(5)
 .
.分析:(1)样本就是研究中实际观测或调查的一部分个体称为样本.依据定义即可解答;
(2)设60~70(分)(含60分,不含70分)的人数为x人,则90分以上(含90分)的人数为(2x+3)人,根据60~70(分)(含60分,不含70分)的人数与90分以上(含90分)的人数的和是21人,即可求得x的值,进而求解;
(3)中位数就是把各个数按从小到大的顺序排列排列,中间即第25与第26两个数的平均数,依据定义即可求解;
(4)求出优良的学生所占的比例,即可求得人数;
(5)求出成绩不低于90分的学生的总人数,根据概率公式,即可求解.
点评:本题考查的知识点较多,有样本的概念,中位数的确定方法,频数与频率的关系,对于每个概念的正确理解是解题关键.用到的知识点为:概率=所求情况数与总情况数之比.一组数据按顺序排列后,中间的那两个数的平均数或中间的那个数叫做中位数.

练习册系列答案
 快捷英语周周练系列答案
快捷英语周周练系列答案
相关题目
 知90分以上(含90分)的人数比60~70分(含60分,不含70分)的人数的2倍还多3人.
知90分以上(含90分)的人数比60~70分(含60分,不含70分)的人数的2倍还多3人.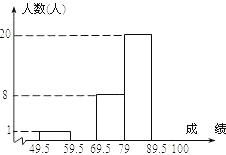 某校为了了解学生对世博礼仪的知晓程度,从全校1200名学生中随机抽取了50名学生进行测试.根据测试成绩(成绩取整数,满分为100分)作了统计分析,绘制成频数分布直方图(如图,其中部分数据缺失).又知90分以上(含90分)的数比60~70分(含60分,不含70分)的人数的2倍还多3人.请你根据上述信息,解答下列问题:
某校为了了解学生对世博礼仪的知晓程度,从全校1200名学生中随机抽取了50名学生进行测试.根据测试成绩(成绩取整数,满分为100分)作了统计分析,绘制成频数分布直方图(如图,其中部分数据缺失).又知90分以上(含90分)的数比60~70分(含60分,不含70分)的人数的2倍还多3人.请你根据上述信息,解答下列问题: