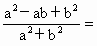题目内容
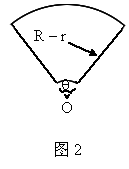
(2007,安徽省芜湖市,22)一园林设计师使用长度为4L的材料建造如图1所示的花圃,该花圃是由四个形状、大小完全一样的扇环面组成,每个扇环面如图2所示,它是以点O为圆心的两个同心圆弧和延长后通过O点的两条直线段围成.为使得绿化效果最佳,还须使扇环面面积最大.
(1)求使图1花圃面积为最大时R-r的值及此花圃面积,其中R、r分别为大圆和小圆的半径;
(2)若L=160m,r=10m,求使图2面积为最大时的θ值.

答案:略
解析:
解析:
|
解: (1)若使形如图1花圃面积为最大,则必定要求图2扇环面积最大.设图 2扇环的圆心角为θ,面积为S,根据题意得:
∴  . .
∴ 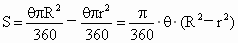
∵式中 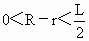 ,∴S在 ,∴S在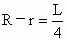 时为最大,最大值为 时为最大,最大值为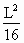 . .
∴花圃面积最大时 R-r值为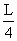 ,最大面积为 ,最大面积为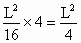 . .
(2) ∵当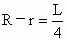 时,S取值最大, 时,S取值最大,
∴ 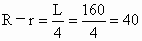 (m),R=40+r=40+10=50(m). (m),R=40+r=40+10=50(m).
∴ 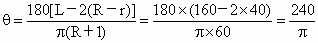 (度). (度). |

练习册系列答案
相关题目
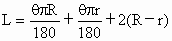
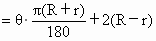
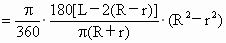
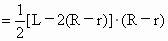
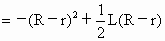
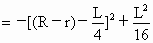

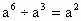
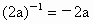

 ,则(2@6)@8=________.
,则(2@6)@8=________. ,则
,则