题目内容
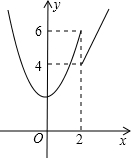 (2012•桐乡市三模)已知函数y=
(2012•桐乡市三模)已知函数y=
|
-
≤x≤4
| 6 |
-
≤x≤4
.| 6 |
分析:把y=8分别代入函数y=2x和y=x2+2,求出对应的x的值,结合图象即可得出答案.
解答:解:①把y=8代入y=2x得:
8=2x,
解得x=4,
即在直线y=2x上,当函数值y≤8时,对应的自变量x的取值范围是x≤4;
②把y=8代入y=x2+2=8,
解得:x=±
,
∵x≤2,
∴x=
舍去,
即根据图象可知,当函数值y≤8时,对应的自变量x的取值范围是x≥-
;
综合①②得出当函数值y≤8时,对应的自变量x的取值范围是-
≤x≤4.
故答案为:-
≤x≤4.
8=2x,
解得x=4,
即在直线y=2x上,当函数值y≤8时,对应的自变量x的取值范围是x≤4;
②把y=8代入y=x2+2=8,
解得:x=±
| 6 |
∵x≤2,
∴x=
| 6 |
即根据图象可知,当函数值y≤8时,对应的自变量x的取值范围是x≥-
| 6 |
综合①②得出当函数值y≤8时,对应的自变量x的取值范围是-
| 6 |
故答案为:-
| 6 |
点评:本题考查了二次函数与不等式(组)的应用,解此题的关键是能根据求出的x的值写出结论,题目比较典型,但是一道比较容易出错的题目.注意数形结合思想的运用.

练习册系列答案
相关题目
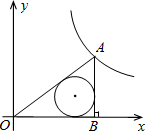 (2012•桐乡市三模)如图,点A(a,b)在双曲线
(2012•桐乡市三模)如图,点A(a,b)在双曲线