题目内容
【题目】将下列推证过程补充完整. 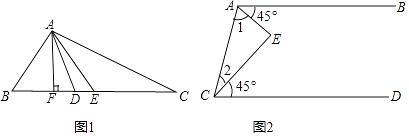
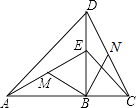
(1)如图1,在△ABC中,AE是中线,AD是角平分线,AF是高.
①BE== ![]() ;
;
②∠BAD== ![]() ;
;
③∠AFB==90°;
④S△ABC= .
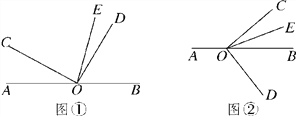
(2)如图2,AB∥CD,∠BAE=∠DCE=45°,
∵AB∥CD
∴∠1+45°+∠2+45°= .
∴∠1+∠2= .
∴∠E= .
【答案】
(1)CE;BC;∠CAD;∠BAC;∠AFC;![]() BC?AF
BC?AF
(2)180°;90°;90°
【解析】解:(1)①BE=CE= ![]() BC;
BC;
②∠BAD=∠CAD= ![]() ∠BAC;
∠BAC;
③∠AFB=∠AFC=90°;
④S△ABC= ![]() BCAF;(2)∵AB∥CD,
BCAF;(2)∵AB∥CD,
∴∠1+45°+∠2+45°=180°,
∴∠1+∠2=90°,
∴∠E=90°.
所以答案是:(1)CE,BC;∠CAD,∠BAC;∠AFC; ![]() BCAF;(2)180°,90°,90°.
BCAF;(2)180°,90°,90°.
【考点精析】关于本题考查的平行线的性质和三角形的“三线”,需要了解两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补;1、三角形角平分线的三条角平分线交于一点(交点在三角形内部,是三角形内切圆的圆心,称为内心);2、三角形中线的三条中线线交于一点(交点在三角形内部,是三角形的几何中心,称为中心);3、三角形的高线是顶点到对边的距离;注意:三角形的中线和角平分线都在三角形内才能得出正确答案.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目