题目内容
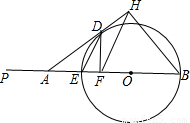
已知,如图,EB是⊙O的直径,且EB=6,在BE的延长线上取点P,使EP=EB,A是EP上一点,过A作⊙O的切线,切点为D,过D作DF⊥AB于F,过B作AD的垂线BH,交AD的延长线于H.当点A在EP上运动,不与E重合时:(1)是否总有
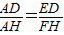 ,试证明你的结论;
,试证明你的结论;(2)设ED=x,BH=y,求y和x的函数关系,并写出x的取值范围.
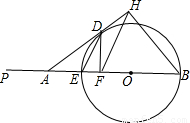
【答案】分析:①欲证所求的比例式,只需证得DE∥FH即可.连接BD,设BD与FH的交点为G,由于HD切⊙O于D,根据弦切角定理知∠HDB=∠DEB,在Rt△DEB中,易证得∠DEB=∠FDB,则∠FDB=∠HDB,即可证得△DFB≌△DHB,由此可得BH=BF,即△BFH是等腰三角形,根据等腰三角形三线合一的性质可证得BD⊥FH,而BD⊥DE,则FH∥DE,由此得证.
②由于BH=BF,根据EB的长,可用y表示出EF的值,进而在Rt△DEB中,根据射影定理得到y、x的函数关系式;求x的取值范围时,只需考虑x的最大值即可,当A、P重合时,若连接OD,则OD⊥PH,根据平行线分线段成比例定理,可求得BH的长,进而可得到BF、EF的值,然后根据射影定理即可求得DE的长,由此求得x的取值范围.
解答:解:①无论点A在EP上怎么移动(点A不与点E重合),
总有 (3分)
(3分)
证明:连接DB,交FH于G.
∵AH是⊙O的切线,∴∠HDB=∠DEB.
又∵BH⊥AH,BE为直径,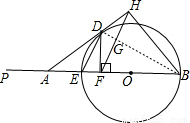
∴∠BDE=90°.
有∠DBE=90°-∠DEB=90°-∠HDB=∠DBH.
在△DFB和△DHB中,
DF⊥AB,∠DFB=∠DHB=90°,
DB=DB,∠DBE=∠DBH,
∴△DFB≌△DHB.(4分)
∴BH=BF.∴△BHF是等腰三角形.
∴BG⊥FH,即BD⊥FH.
∴ED∥FH,∴ (5分)
(5分)
②∵ED=x,BH=y,BE=6,BF=BH,
∴EF=6-y,
又∵DF是Rt△BDE斜边上的高,
∴△DFE∽△BDE,
∴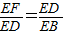
即ED2=EF•EB.
∴x2=6(6-y)即y=- x2+6(7分)
x2+6(7分)
∴ED=x>0,
当A从E向左移动,ED逐渐增大,
当A和P重合时,ED最大,
这时,连接OD,则OD⊥PH,
∴OD∥BH.
又PO=PE+EO=6+3=9,PB=12,
 ,BH=
,BH=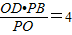
∴BF=BH=4,EF=EB-BF=6-4=2.
由ED2=EF•EB,得:x2=2×6=12,
∵x>0,∴x=2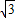 ,
,
∴0<x≤2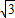 ,
,
[或由BH=4=y,代入y=- x2+6中,得x=2
x2+6中,得x=2  ]
]
故所求函数关系式为y=- x2+6(0<x≤2
x2+6(0<x≤2  ).
).
点评:此题主要考查了切线的性质、圆周角定理、全等三角形及相似三角形的判定和性质、平行线的判定等知识;(2)①中,能够构造出与所求相关的全等三角形是解决问题的关键.
②由于BH=BF,根据EB的长,可用y表示出EF的值,进而在Rt△DEB中,根据射影定理得到y、x的函数关系式;求x的取值范围时,只需考虑x的最大值即可,当A、P重合时,若连接OD,则OD⊥PH,根据平行线分线段成比例定理,可求得BH的长,进而可得到BF、EF的值,然后根据射影定理即可求得DE的长,由此求得x的取值范围.
解答:解:①无论点A在EP上怎么移动(点A不与点E重合),
总有
 (3分)
(3分)证明:连接DB,交FH于G.
∵AH是⊙O的切线,∴∠HDB=∠DEB.
又∵BH⊥AH,BE为直径,

∴∠BDE=90°.
有∠DBE=90°-∠DEB=90°-∠HDB=∠DBH.
在△DFB和△DHB中,
DF⊥AB,∠DFB=∠DHB=90°,
DB=DB,∠DBE=∠DBH,
∴△DFB≌△DHB.(4分)
∴BH=BF.∴△BHF是等腰三角形.
∴BG⊥FH,即BD⊥FH.
∴ED∥FH,∴
 (5分)
(5分)②∵ED=x,BH=y,BE=6,BF=BH,
∴EF=6-y,
又∵DF是Rt△BDE斜边上的高,
∴△DFE∽△BDE,
∴
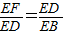
即ED2=EF•EB.
∴x2=6(6-y)即y=-
 x2+6(7分)
x2+6(7分)∴ED=x>0,
当A从E向左移动,ED逐渐增大,
当A和P重合时,ED最大,
这时,连接OD,则OD⊥PH,

∴OD∥BH.
又PO=PE+EO=6+3=9,PB=12,
 ,BH=
,BH=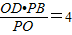
∴BF=BH=4,EF=EB-BF=6-4=2.
由ED2=EF•EB,得:x2=2×6=12,
∵x>0,∴x=2
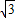 ,
,∴0<x≤2
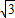 ,
,[或由BH=4=y,代入y=-
 x2+6中,得x=2
x2+6中,得x=2  ]
]故所求函数关系式为y=-
 x2+6(0<x≤2
x2+6(0<x≤2  ).
).点评:此题主要考查了切线的性质、圆周角定理、全等三角形及相似三角形的判定和性质、平行线的判定等知识;(2)①中,能够构造出与所求相关的全等三角形是解决问题的关键.

练习册系列答案
相关题目
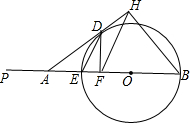 O的切线AD,切点为D.过D作DF⊥AB于F,过B作AD的垂线BH,交AD的延长线于H.连接ED和FH.
O的切线AD,切点为D.过D作DF⊥AB于F,过B作AD的垂线BH,交AD的延长线于H.连接ED和FH.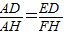 ?试证明你的结论;
?试证明你的结论;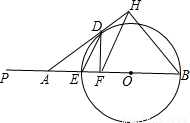
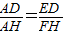 ?试证明你的结论;
?试证明你的结论;