题目内容

正三角形ABC的边长BC=2，以该等边三角形的高AD为正方形的边长，则正方形的面积为________．

3
分析：根据等边三角形三线合一的性质可得D为BC的中点，即BD=CD，在直角三角形ABD中，已知AB、BD，根据勾股定理即可求得AD的长，即可求正方形的面积，即可解题．
解答：∵等边三角形三线合一，
∴D为BC的中点，即BD=DC=1，
∴AD=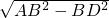 $\text{[math]}$ = $\text{[math]}$ ，
∴正方形的面积为 $\text{[math]}$ × $\text{[math]}$ =3．
故答案为3．
点评：本题考查了勾股定理在直角三角形中的运用，正方形面积的计算，本题中根据勾股定理计算AD的值是解题的关键．

练习册系列答案

金牌教辅培优优选卷期末冲刺100分系列答案

中考专项突破系列答案

全能金卷小学毕业升学全程总复习系列答案

新课程同步导学练测八年级英语下册系列答案

精致课堂有效反馈系列答案

小考状元必备测试卷系列答案

全能小考王小升初名校备考密卷系列答案

中考5月冲关卷系列答案

中考5加3预测卷系列答案

升学考试一本通系列答案

相关题目

（2012•陕西）如图，正三角形ABC的边长为3+

．
（1）如图①，正方形EFPN的顶点E、F在边AB上，顶点N在边AC上，在正三角形ABC及其内部，以点A为位似中心，作正方形EFPN的位似正方形E′F′P′N′，且使正方形E′F′P′N′的面积最大（不要求写作法）；
（2）求（1）中作出的正方形E′F′P′N′的边长；
（3）如图②，在正三角形ABC中放入正方形DEMN和正方形EFPH，使得DE、EF在边AB上，点P、N分别在边CB、CA上，求这两个正方形面积和的最大值和最小值，并说明理由．

正三角形ABC的边长为3cm，一个边长是1cm的正方形EFMN的顶点N与B重合，将正方形如图①所示放置．然后将正方形绕N点顺时针方向旋转，使E点落在AB上，如图②，再将正方形绕E点顺时针方向旋转，使F点落在AB上，如图③…，按照这样的方式旋转下去，直到小正方形有一顶点与B点重合为止，这时小正方形与B点重合的点是

；小正方形一共旋转的度数是

（2013•昌平区二模）正三角形ABC的边长为2，动点P从点A出发，以每秒1个单位长度的速度，沿A→B→C→A的方向运动，到达点A时停止．设运动时间为x秒，y=PC²，则y关于x的函数的图象大致为（　　）

（2013•大庆）正三角形△ABC的边长为3，依次在边AB、BC、CA上取点A₁、B₁、C₁，使AA₁=BB₁=CC₁=1，则△A₁B₁C₁的面积是（　　）

如图，正三角形ABC的边长为4cm，分别以A、B、C为圆心画圆，三个圆两两相切，切点分别为D、E、F，则图中阴影部分面积是（　　）