题目内容
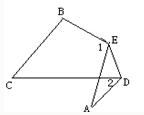
 如图,把△ABC纸片沿DE折叠,点A落在四边形BCDE的内部,则
如图,把△ABC纸片沿DE折叠,点A落在四边形BCDE的内部,则
- A.∠A=∠1+∠2
- B.2∠A=∠1+∠2
- C.3∠A=2∠1+∠2
- D.3∠A=2(∠1+∠2)
B
分析:根据折叠的性质∠FED=∠AED,∠FDE=∠ADE,根据三角形内角和定理和邻补角的定义即可表示出∠A、∠1、∠2之间的关系.
解答: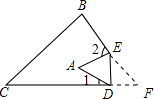 解:根据题意得∠FED=∠AED,∠FDE=∠ADE,
解:根据题意得∠FED=∠AED,∠FDE=∠ADE,
由三角形内角和定理可得,∠FED+∠EDF=180°-∠F=180°-∠A,
∴∠AEF+∠ADF=2(180°-∠A),
∴∠1+∠2=360°-(∠AEF+∠ADF)=360°-2(180°-∠A)=2∠A.
所以2∠A=∠1+∠2.
故选B.
点评:本题主要考查了三角形的内角和定理和邻补角的定义,需要熟练掌握.
分析:根据折叠的性质∠FED=∠AED,∠FDE=∠ADE,根据三角形内角和定理和邻补角的定义即可表示出∠A、∠1、∠2之间的关系.
解答:
 解:根据题意得∠FED=∠AED,∠FDE=∠ADE,
解:根据题意得∠FED=∠AED,∠FDE=∠ADE,由三角形内角和定理可得,∠FED+∠EDF=180°-∠F=180°-∠A,
∴∠AEF+∠ADF=2(180°-∠A),
∴∠1+∠2=360°-(∠AEF+∠ADF)=360°-2(180°-∠A)=2∠A.
所以2∠A=∠1+∠2.
故选B.
点评:本题主要考查了三角形的内角和定理和邻补角的定义,需要熟练掌握.

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目
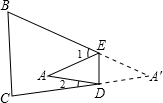 如图,把△ABC纸片沿DE折叠,当点A落在四边形BCDE内部时,
如图,把△ABC纸片沿DE折叠,当点A落在四边形BCDE内部时,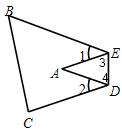
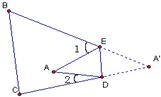
 20、如图,把△ABC纸片沿DE折叠,当点A落在四边形BCDE的外部时,∠A与∠1、∠2之间存在一种始终保持不变的数量关系,这个数量关系是
20、如图,把△ABC纸片沿DE折叠,当点A落在四边形BCDE的外部时,∠A与∠1、∠2之间存在一种始终保持不变的数量关系,这个数量关系是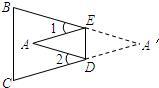 如图,把△ABC纸片沿DE折叠,当点A落在四边形BCDE内部时,
如图,把△ABC纸片沿DE折叠,当点A落在四边形BCDE内部时,