题目内容
(按非课改要求命制)如图,CD是⊙O的弦,点P在弦CD上,点A是弧CD的中点,过点P作PA⊥OP交⊙O于点A,已知,CP=2cm,PD=8cm,则PA= cm.
【答案】分析:由于点A是弧CD的中点,所以AO与CD垂直,又因为CP=2cm,PD=8cm,所以CD=10cm,CM=5,根据勾股定理,设OC=r,OM=x,则r2-x2=25,在△OPM中,OP2=x2+9,由于PA⊥OP,所以OP2+AP2=r2,联立以上三个式子,即可求出AP=4.
解答: 解:如图,连接OA,OC.
解:如图,连接OA,OC.
∵点A是弧CD的中点,
AO⊥CD,
又∵CP=2cm,PD=8cm,
∴CD=10cm,CM=5cm,
根据勾股定理,设OC=r,OM=x,
则r2-x2=25,①
在△OPM中,OP2=x2+9,②
∵PA⊥OP,
∴OP2+AP2=r2,③
联立①②③,
即可求出AP=4cm.
点评:解决与弦有关的问题时,往往需构造以半径、弦心距和弦长的一半为三边的直角三角形,若设圆的半径为r,弦长为a,这条弦的弦心距为d,则有等式r2=d2+( )2成立,知道这三个量中的任意两个,就可以求出另外一个.
)2成立,知道这三个量中的任意两个,就可以求出另外一个.
解答:
 解:如图,连接OA,OC.
解:如图,连接OA,OC.∵点A是弧CD的中点,
AO⊥CD,
又∵CP=2cm,PD=8cm,
∴CD=10cm,CM=5cm,
根据勾股定理,设OC=r,OM=x,
则r2-x2=25,①
在△OPM中,OP2=x2+9,②
∵PA⊥OP,
∴OP2+AP2=r2,③
联立①②③,
即可求出AP=4cm.
点评:解决与弦有关的问题时,往往需构造以半径、弦心距和弦长的一半为三边的直角三角形,若设圆的半径为r,弦长为a,这条弦的弦心距为d,则有等式r2=d2+(
 )2成立,知道这三个量中的任意两个,就可以求出另外一个.
)2成立,知道这三个量中的任意两个,就可以求出另外一个. 
练习册系列答案
相关题目
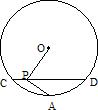 17、(按非课改要求命制)如图,CD是⊙O的弦,点P在弦CD上,点A是弧CD的中点,过点P作PA⊥OP交⊙O于点A,已知,CP=2cm,PD=8cm,则PA=
17、(按非课改要求命制)如图,CD是⊙O的弦,点P在弦CD上,点A是弧CD的中点,过点P作PA⊥OP交⊙O于点A,已知,CP=2cm,PD=8cm,则PA=