题目内容
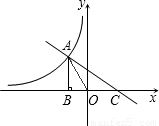
如图,直线AC与双曲线y=| k |
| x |
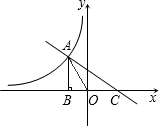 O|=4,点A的横坐标为-2,过点A作AB⊥x轴于点B,且S△AOC:S△AOB=3:2.
O|=4,点A的横坐标为-2,过点A作AB⊥x轴于点B,且S△AOC:S△AOB=3:2.(1)求k的值及直线AC的解析式;
(2)在第二象限内双曲线y=
| k |
| x |
分析:(1)∵|AO|=4,点A的横坐标为-2,即OB=2,得到∠BAO=30°,则AB=
OB=2
,确定A点坐标为(-2,2
),于是可求得k=-2×2
=-4
;再根据S△AOC:S△AOB=3:2,得到OC:OB=3:2,而OB=2,求出OC=3,得到C点坐标为(3,0),然后利用待定系数法即可求出直线AC的解析式;
(2)点P(r,m)在反比例函数图象上得到m=-
,r<0,m>0,再根据三角形的面积公式得S=
•BC•m=
•5•(-
),整理即可.
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
(2)点P(r,m)在反比例函数图象上得到m=-
4
| ||
| r |
| 1 |
| 2 |
| 1 |
| 2 |
4
| ||
| r |
解答:解:(1)∵|AO|=4,点A的横坐标为-2,即OB=2,
∴∠BAO=30°,
∴AB=
OB=2
,
∴A点坐标为(-2,2
),
∴k=-2×2
=-4
,
∵S△AOC:S△AOB=3:2,
∴OC:OB=3:2,而OB=2,
∴OC=3,
∴C点坐标为(3,0),
设直线AC的解析式为y=kx+b,
把A(-2,2
),C(3,0)代入得,-2k+b=2
,3k+b=0,解得k=-
,b=
,
∴直线AC的解析式为:y=-
x+
;
(2)双曲的解析式为y=-
,
∵点P(r,m)在反比例函数图象上,
∴m=-
,r<0,m>0,
∴S=
•BC•m
=
•5•(-
)
=-
.
∴S与r的函数关系式为S=-
(r<0).
∴∠BAO=30°,
∴AB=
| 3 |
| 3 |
∴A点坐标为(-2,2
| 3 |
∴k=-2×2
| 3 |
| 3 |
∵S△AOC:S△AOB=3:2,
∴OC:OB=3:2,而OB=2,
∴OC=3,
∴C点坐标为(3,0),
设直线AC的解析式为y=kx+b,
把A(-2,2
| 3 |
| 3 |
2
| ||
| 5 |
6
| ||
| 5 |
∴直线AC的解析式为:y=-
2
| ||
| 5 |
6
| ||
| 5 |
(2)双曲的解析式为y=-
4
| ||
| x |
∵点P(r,m)在反比例函数图象上,
∴m=-
4
| ||
| r |
∴S=
| 1 |
| 2 |
=
| 1 |
| 2 |
4
| ||
| r |
=-
10
| ||
| r |
∴S与r的函数关系式为S=-
10
| ||
| r |
点评:本题考查了已知一点的坐标确定反比例函数图象的解析式.也考查了利用待定系数法求直线的解析式的方法以及三角形的面积公式.

练习册系列答案
相关题目
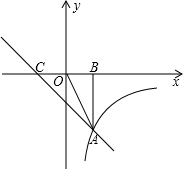 点A的横坐标为2,过点A作AB⊥x轴于点B,且S△ABC:S△ABO=4:1.
点A的横坐标为2,过点A作AB⊥x轴于点B,且S△ABC:S△ABO=4:1.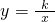 在第二象限交于点A(x0,y0),交x轴的正半轴于点C,且|A
在第二象限交于点A(x0,y0),交x轴的正半轴于点C,且|A O|=4,点A的横坐标为-2,过点A作AB⊥x轴于点B,且S△AOC:S△AOB=3:2.
O|=4,点A的横坐标为-2,过点A作AB⊥x轴于点B,且S△AOC:S△AOB=3:2.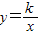 在第二象限交于点A(x,y),交x轴的正半轴于点C,且|AO|=4,点A的横坐标为-2,过点A作AB⊥x轴于点B,且S△AOC:S△AOB=3:2.
在第二象限交于点A(x,y),交x轴的正半轴于点C,且|AO|=4,点A的横坐标为-2,过点A作AB⊥x轴于点B,且S△AOC:S△AOB=3:2. 上有一动点P(r,m),设△BCP的面积为S.求S与r的函数关系式.
上有一动点P(r,m),设△BCP的面积为S.求S与r的函数关系式.