题目内容
【题目】在x轴上有点P(a,0)(其中a>2),过点P作x斜的蓬线,分别交函数 ![]() 和
和 ![]() 的图象于点C、D。
的图象于点C、D。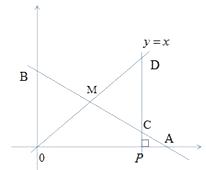
(1)求点A的坐标
(2)若OB=CD,求a的值
(3)在(2)条件下若以0D线段为边,作正方形0DEF,求直线EF的表达式。
【答案】
(1)解:∵点M在直线y=x的图象上,且点M的横坐标为2,
∴点M的坐标为(2,2),
把M(2,2)代入y=-![]() x+b得-1+b=2,解得b=3,
x+b得-1+b=2,解得b=3,
∴一次函数的解析式为y=-x+3,
把y=0代入y=-![]() x+3得-
x+3得-![]() x+3=0,解得x=6,
x+3=0,解得x=6,
∴A点坐标为(6,0);
(2)把x=0代入y=-1
2x+3得y=3,
∴B点坐标为(0,3),
∵CD=OB,
∴CD=3,
∵PC⊥x轴,
∴C点坐标为(a,-![]() a+3),D点坐标为(a,a)
a+3),D点坐标为(a,a)
∴a-(-![]() a+3)=3,
a+3)=3,
∴a=4.
(3)由(2)知,OD=4![]() ,∵四边形ODEF为正方形,∴EF
,∵四边形ODEF为正方形,∴EF![]() OD,且EF=OD,直线EF相当于直线OD向下平移8个单位得到的,∴直线EF 的表达式为y=x-8.
OD,且EF=OD,直线EF相当于直线OD向下平移8个单位得到的,∴直线EF 的表达式为y=x-8.
【解析】(1)先利用直线y=x上的点的坐标特征得到点M的坐标为(2,2),再把M(2,2)代入y=-1
2x+b可计算出b=3,得到一次函数的解析式为y=-![]() x+3,然后根据x轴上点的坐标特征可确定A点坐标为(6,0);
x+3,然后根据x轴上点的坐标特征可确定A点坐标为(6,0);
(2)先确定B点坐标为(0,3),则OB=CD=3,再表示出C点坐标为(a,-![]() a+3),D点坐标为(a,a),所以a-(-
a+3),D点坐标为(a,a),所以a-(-![]() a+3)=3,然后解方程即可
a+3)=3,然后解方程即可
(3)利用正方形的性质,OD 平行且等于EF,可利用平移关系求出EF的表达式.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目