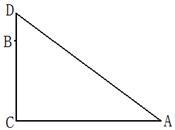
题目内容
如图,在一棵树的10米高B处有三只猴子,第一只猴子爬下树走到离树20米处的池塘A处,第二只猴子直接从B处跃到A处,第三只爬到树顶D后直接跃到A处,距离以直线计算,假设其中两只猴子所经过的距离相等.(1)求第二只猴子经过的直线距离;
(2)求这棵树的高度.
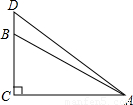
【答案】分析:(1)直接利用勾股定理求得线段BA的长即可;
(2)由题意知AD+DB=BC+CA,设BD=x,则AD=30-x,且在直角△ACD中,CD2+CA2=AD2,代入勾股定理公式中即可求x的值,树高CD=10+x.
解答:解:(1)由题意知:在Rt△ABC中,BC=10米,AC=20米,
由勾股定理得:BA=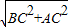 =
=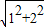 =10
=10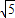 .
.
故第二只猴子经过的直线距离是10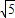 米;
米;
(2)由题意知AD+DB=BC+CA,且CA=20米,BC=10米,
设BD=x,则AD=30-x,
∵在Rt△ACD中:CD2+CA2=AD2,
即(30-x)2=(10+x)2+202,
解得x=5米,
故树高为CD=10+x=15米.
答:树高为15米.
点评:本题考查了勾股定理及一元二次方程在实际生活中的应用,本题中找到AD+DB=BC+CA的等量关系,并根据勾股定理CD2+CA2=AD2求解是解题的关键.
(2)由题意知AD+DB=BC+CA,设BD=x,则AD=30-x,且在直角△ACD中,CD2+CA2=AD2,代入勾股定理公式中即可求x的值,树高CD=10+x.
解答:解:(1)由题意知:在Rt△ABC中,BC=10米,AC=20米,
由勾股定理得:BA=
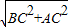 =
=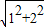 =10
=10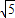 .
.故第二只猴子经过的直线距离是10
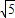 米;
米;(2)由题意知AD+DB=BC+CA,且CA=20米,BC=10米,
设BD=x,则AD=30-x,
∵在Rt△ACD中:CD2+CA2=AD2,
即(30-x)2=(10+x)2+202,
解得x=5米,
故树高为CD=10+x=15米.
答:树高为15米.
点评:本题考查了勾股定理及一元二次方程在实际生活中的应用,本题中找到AD+DB=BC+CA的等量关系,并根据勾股定理CD2+CA2=AD2求解是解题的关键.

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
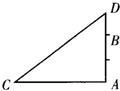
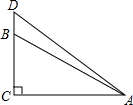 如图,在一棵树的10米高B处有三只猴子,第一只猴子爬下树走到离树20米处的池塘A处,第二只猴子直接从B处跃到A处,第三只爬到树顶D后直接跃到A处,距离以直线计算,假设其中两只猴子所经过的距离相等.
如图,在一棵树的10米高B处有三只猴子,第一只猴子爬下树走到离树20米处的池塘A处,第二只猴子直接从B处跃到A处,第三只爬到树顶D后直接跃到A处,距离以直线计算,假设其中两只猴子所经过的距离相等.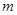 高B处有2只猴子,一只猴子爬到树下走到离树20
高B处有2只猴子,一只猴子爬到树下走到离树20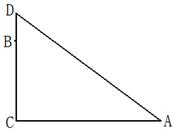
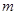 高B处有2只猴子,一只猴子爬到树下走到离树20
高B处有2只猴子,一只猴子爬到树下走到离树20