题目内容
【题目】为了提高服务质量,某宾馆决定对甲、乙两种套房进行星级提升,已知甲种套房提升费用比乙种套房提升费用少3万元,如果提升相同数量的套房,甲种套房费用为625万元,乙种套房费用为700万元.
(1)甲、乙两种套房每套提升费用各多少万元?
(2)如果需要甲、乙两种套房共80套,市政府筹资金不少于2090万元,但不超过2096万元,且所筹资金全部用于甲、乙种套房星级提升,市政府对两种套房的提升有几种方案?哪一种方案的提升费用最少?
(3)在(2)的条件下,根据市场调查,每套乙种套房的提升费用不会改变,每套甲种套房提升费用将会提高a万元(a>0),市政府如何确定方案才能使费用最少?
【答案】(1)甲,乙两种套房每套提升费用分别为25万元,28万元.(2) 有三种方案分别是:方案一:甲种套房提升48套,乙种套房提升32套.方案二:甲种套房提升49套,乙种套房提升31套,方案三:甲种套房提升50套,乙种套房提升30套.第三种方案费用最少.(3) 当a=3时,三种方案的费用一样,都是2240万元.当a>3时,m=48时,费用W最小.当0<a<3时,, m=50时,W最小,费用最省.
【解析】
试题分析:(1)设甲种套房每套提升费用为x万元,根据题意建立方程求出其解即可;
(2)设甲种套房提升m套,那么乙种套房提升(80-m)套,根据条件建立不等式组求出其解就可以求出提升方案,再表示出总费用与m之间的函数关系式,根据一次函数的性质就可以求出结论;
(3)根据(2)表示出W与m之间的关系式,由一次函数的性质分类讨论就可以得出结论.
试题分析:(1)设甲种套房每套提升费用为x万元,依题意,
得![]() 解得:x=25
解得:x=25
经检验:x=25符合题意,x+3=28
答:甲,乙两种套房每套提升费用分别为25万元,28万元.
(2)设甲种套房提升m套,那么乙种套房提升(80-m)套,依题意,得
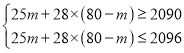
解得:48≤m≤50
即m=48或49或50,所以有三种方案分别是:
方案一:甲种套房提升48套,乙种套房提升32套.
方案二:甲种套房提升49套,乙种套房提升31套,
方案三:甲种套房提升50套,乙种套房提升30套.
设提升两种套房所需要的费用为W元.则
W=25m+28×(80-m)=-3m+2240,
∵k=-3<0,
∴W随m的增大而减小,
∴当m=50时,W最少=2090元,即第三种方案费用最少.
(3)在(2)的基础上有:W=(25+a)m+28×(80-m)=(a-3)m+2240
当a=3时,三种方案的费用一样,都是2240万元.
当a>3时,k=a-3>0,
∴W随m的增大而增大,
∴m=48时,费用W最小.
当0<a<3时,k=a-3<0,
∴W随m的增大而减小,
∴m=50时,W最小,费用最省.

 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案