题目内容
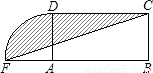
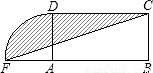
设计一个商标图案如图中阴影部分,矩形ABCD中,AB=2BC,且AB=8cm,以点A为圆心,AD为半径作圆与BA的延长线相交于点F,则商标图案的面积等于( )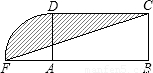
A.(4π+8)cm2
B.(4π+16)cm2
C.(3π+8)cm2
D.(3π+16)cm2
【答案】分析:阴影面积=S△ADC+S扇形ADF-S△AFC.
解答: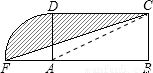 解:连接AC.
解:连接AC.
∵S△ADC=8×4÷2=16;
S扇形ADF= =4π;
=4π;
S△AFC=4×4÷2=8,
∴阴影面积=S△ADC+S扇形ADF-S△AFC=(4π+8)cm2.
故选A.
点评:解决本题的关键是得到所求的量的等量关系.
解答:
 解:连接AC.
解:连接AC.∵S△ADC=8×4÷2=16;
S扇形ADF=
 =4π;
=4π;S△AFC=4×4÷2=8,
∴阴影面积=S△ADC+S扇形ADF-S△AFC=(4π+8)cm2.
故选A.
点评:解决本题的关键是得到所求的量的等量关系.

练习册系列答案
相关题目
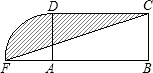 设计一个商标图案如图中阴影部分,矩形ABCD中,AB=2BC,且AB=8cm,以点A为圆心,AD为半径作圆与BA的延长线相交于点F,则商标图案的面积等于( )
设计一个商标图案如图中阴影部分,矩形ABCD中,AB=2BC,且AB=8cm,以点A为圆心,AD为半径作圆与BA的延长线相交于点F,则商标图案的面积等于( )| A、(4π+8)cm2 | B、(4π+16)cm2 | C、(3π+8)cm2 | D、(3π+16)cm2 |
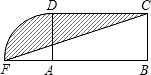 设计一个商标图案如图中阴影部分,矩形ABCD中,AB=2BC,且AB=8cm,以点A为圆心,AD为半径作圆与BA的延长线相交于点F,则商标图案的面积等于
设计一个商标图案如图中阴影部分,矩形ABCD中,AB=2BC,且AB=8cm,以点A为圆心,AD为半径作圆与BA的延长线相交于点F,则商标图案的面积等于