题目内容
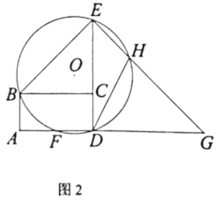
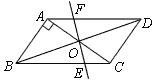
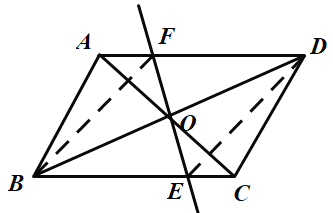
【题目】如图，平行四边形ABCD中，AB⊥AC，AB=
，BC=
,对角线AC，BD相交于点O，将直线AC绕点O顺时针旋转，分别交BC，AD于点E，F,下列说法：①在旋转过程中，AF=CE. ②OB=AC，③在旋转过程中，四边形ABEF的面积为
，④当直线AC绕点O顺时针旋转30°时，连接BF,DE则四边形BEDF是菱形，其中正确的是（ ）
A.①②④B.① ②C.①②③④D.② ③ ④
【答案】A
【解析】
①通过证明
即可判断；
②分别利用勾股定理求出OB,AC的长度即可得出答案；
③先利用
的面积求出AG的长度，然后利用梯形的面积公式求解即可；
④易证四边形BEDF是平行四边形，然后通过角度得出
，然后证明
，则有
，则可证明结论．
∵四边形ABCD是平行四边形，
，
．
在
和
中，
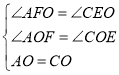
，故①正确；
∵AB⊥AC，
．
∵AB=
，BC=
，
，
，
，
，故②正确；
过点A作
交BC于点G，
，
，
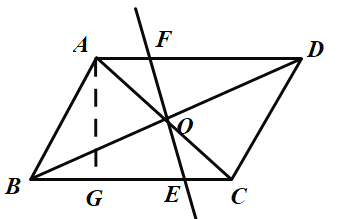
，故③错误；
连接DE,BF，
，
．
∵
，
∴四边形BEDF是平行四边形．
，
．
，
，
．
在
和
中，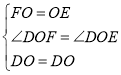
，
，
∴四边形BEDF是菱形，故④正确；
所以正确的有：①②④，
故选：A．
【题目】某乒乓球馆使用发球机进行辅助训练，出球口在桌面中线端点A处的正上方，假设每次发出的乒乓球的运动路线固定不变，且落在中线上，在乒乓球运行时，设乒乓球与端点A的水平距离为x（米），与桌面的高度为y（米），经多次测试后，得到如下部分数据：
x/米 | 0 | 0.2 | 0.4 | 0.6 | 1 | 1.4 | 1.6 | 1.8 | … |
y/米 | 0.24 | 0.33 | 0.4 | 0.45 | 0.49 | 0.45 | 0.4 | 0.33 | … |
（1）由表中的数据及函数学习经验，求出y关于x的函数解析式；
（2）试求出当乒乓球落在桌面时，其落点与端点A的水平距离是多少米？
（3）当乒乓球落在桌面上弹起后，y与x之间满足
．
①用含a的代数式表示k；
②已知球网高度为0.14米，球桌长（1.4×2）米．若a=-0.5，那么乒乓球弹起后，是否有机会在某个击球点可以将球沿直线扣杀到端点A？请说明理由．
