题目内容
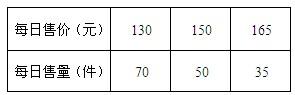
成本是120元的某产品,售价与售量之间存在着下表的数量关系,但每天的利润不相同,为确立产品的最佳定价m元,在定价m元时,每天利润达最佳数1600元,请你确定m的值.
| 每日售价(元) | 130 | 150 | 165 |
| 每日售量(件) | 70 | 50 | 35 |
解:由表中提供信息可知:售价每提高一元,少售一件.
∴定价m元时,有(m-120)[80-(m-120)]=1600,
解之得m=160,
即每件为160元.
分析:售价由130变为150,那么销售量由70减为50,可得售价每提高一元,少售一件;那么售价为120元时,应售出70+10=80件.等量关系为:(每件的售价-成本)×(80-高于120的售价)=1600.把相关数值代入求正数解即可.
点评:考查一元二次方程的应用;得到每件产品的利润及可卖出产品的销售量是解决本题的突破点.
∴定价m元时,有(m-120)[80-(m-120)]=1600,
解之得m=160,
即每件为160元.
分析:售价由130变为150,那么销售量由70减为50,可得售价每提高一元,少售一件;那么售价为120元时,应售出70+10=80件.等量关系为:(每件的售价-成本)×(80-高于120的售价)=1600.把相关数值代入求正数解即可.
点评:考查一元二次方程的应用;得到每件产品的利润及可卖出产品的销售量是解决本题的突破点.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
成本是120元的某产品,售价与售量之间存在着下表的数量关系,但每天的利润不相同,为确立产品的最佳定价m元,在定价m元时,每天利润达最佳数1600元,请你确定m的值.
|
每日售价(元) |
130 |
150 |
165 |
|
每日售量(件) |
70 |
50 |
35 |
成本是120元的某产品,售价与售量之间存在着下表的数量关系,但每天的利润不相同,为确立产品的最佳定价m元,在定价m元时,每天利润达最佳数1600元,请你确定m的值.
| 每日售价(元) | 130 | 150 | 165 |
| 每日售量(件) | 70 | 50 | 35 |