题目内容
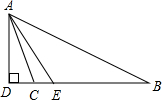 如图,∠ADB=90°,AE平分∠BAD,∠B=30°,∠ACD=70°,则∠CAE=
如图,∠ADB=90°,AE平分∠BAD,∠B=30°,∠ACD=70°,则∠CAE=10
10
°.分析:根据直角三角形的两个锐角互余,得∠BAD=60°,根据角平分线定义求得∠EAB;根据三角形的外角的性质,求得∠BAC,从而求得∠CAE.
解答:解:∵AD⊥BD,∠B=30°,
∴∠BAD=60°.
又∵AE平分∠BAD,
∴∠EAB=30°.
∵∠ACD=70°,
∴∠BAC=∠ACD-∠B=40°.
∴∠CAE=∠BAC-∠EAB=10°.
故答案为:10.
∴∠BAD=60°.
又∵AE平分∠BAD,
∴∠EAB=30°.
∵∠ACD=70°,
∴∠BAC=∠ACD-∠B=40°.
∴∠CAE=∠BAC-∠EAB=10°.
故答案为:10.
点评:此题综合运用了三角形的内角和定理、三角形的外角性质以及角平分线定义.三角形的内角和是180°;三角形的外角等于和它不相邻的两个内角的和.

练习册系列答案
相关题目
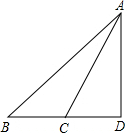 如图,∠ADB=90°,则AD
如图,∠ADB=90°,则AD 如图,∠ADB=90°,AE平分∠BAD,∠B=30°,∠ACD=70°,则∠CAE=________°.
如图,∠ADB=90°,AE平分∠BAD,∠B=30°,∠ACD=70°,则∠CAE=________°. 如图,∠ADB=90°,则AD________BD;用“<”连接AB,AC,AD,结果是________.
如图,∠ADB=90°,则AD________BD;用“<”连接AB,AC,AD,结果是________.