Question

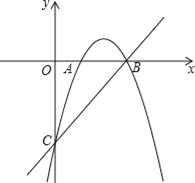
【题目】在平面直角坐标系xOy中，抛物线y=﹣x2+bx+c与x轴交于A、B两点（点A在点B的左侧），与y轴交于点C，点B的坐标为（3，0），直线y=kx﹣3经过B、C两点．

（1）求k的值既抛物线的函数表达式；

（2）如果P是线段BC上一点，设△ABP、△APC的面积分别为S△ABP、S△APC，且S△ABP：S△APC=2：3，求点P的坐标；

（3）设⊙Q的半径为1，圆心Q在抛物线上运动，则在运动过程中是否存在⊙O与坐标轴相切的情况？若存在，求出圆心Q的坐标；若不存在，请说明理由，并探究：若设⊙Q的半径为r，圆心Q在抛物线上运动，则当r取何值时，⊙Q与两坐标轴同时相切？

Answer 1

【答案】（1）y=﹣x2+4x﹣3；（2）P点的纵坐标为（，﹣）；（3）①Q点的坐标为（﹣1，8）；

②存在⊙Q与坐标轴相切，圆心Q的坐标为（1，0），（﹣1，8），（2+，﹣1），（2﹣，﹣1）；

③当r=时，⊙Q与两坐标轴同时相切．

【解析】

（1）根据待定系数法，可得函数解析式；

（2）根据面积的比，可得PB∶PC的值，根据相似三角形的判定与性质，可得PD的长，根据自变量与函数值的对应关系，可得答案；

（3）根据圆与坐标轴相切，可得x或y的值，再根据自变量与函数值的对应关系，可得Q点坐标.

（1）将B点坐标代入y=kx﹣3，得3k﹣3=0，解得k=1；

直线的解析式为y=x﹣3，当x=0时，y=﹣3，即C点坐标为（0，﹣3），

将B、C点坐标代入抛物线的解析式，解得b=4，c=﹣3，

抛物线的解析式为y=﹣x2+4x﹣3；

（2）作PD⊥AB于D点，如图：

由S△ABP：S△APC=2：3，得PB：PC=2：3，PB：BC=2：5．

由△PBD∽△COB，得=，解得DP=，

解得P点的纵坐标为﹣，当y=﹣时，x﹣3=﹣，解得x=，

得P点的纵坐标为（，﹣）；

（3）设Q（x，y），

①当⊙Q与y轴相切时，有|x|=1，即x=±1．

当x=1时，y=﹣x2+4x﹣3=0，即Q点的坐标为（1，0），

当x=﹣1时，y=﹣x2+4x﹣3=﹣8，得Q点的坐标为（﹣1，8）；

②当⊙Q与x轴相切时，有|y|=1，即y=±1．

当y=1时，1=﹣x2+4x﹣3，解得x=2，即Q点的坐标为（2，1）；

当y=﹣1时，﹣1=﹣x2+4x﹣3，解得x=2，即Q（2+，﹣1），（2﹣，﹣1），

综上所述：存在⊙Q与坐标轴相切，圆心Q的坐标为（1，0），（﹣1，8），（2+，﹣1），（2﹣，﹣1）；

③当⊙Q与两坐标轴同时相切时，有|x|=|y|．

当y=x时，﹣x2+4x﹣3=x，此方程无解；

当y=﹣x时，﹣x2+4x﹣3=﹣x，解得x=，当r=时，⊙Q与两坐标轴同时相切，

综上所述：当r=时，⊙Q与两坐标轴同时相切．