题目内容
如图,在同一平面内将两个全等的等腰直角三角形ABC和AFG摆放在一起,A为公共顶点,∠BAC=∠AFG=90°,它们的斜边长为2,若△ABC固定不动,△AFG绕点A旋转,AF、AG与边BC的交点分别为D、E(点D不与点B重合,点E不与点C重合)
(1)求证:△ABE∽△DCA.
(2)若BD=
,求CE.

(1)求证:△ABE∽△DCA.
(2)若BD=
| 1 | 2 |
分析:(1)由图形得∠BAE=∠BAD+45°,由外角定理,得∠CDA=∠BAD+45°,可得∠BAE=∠CDA,根据∠B=∠C=45°,证明两个三角形相似;
(2)由勾股定理,得CA=BA=
,由(1)的相似三角形的性质,利用相似比即可求出CE.
(2)由勾股定理,得CA=BA=
| 2 |
解答:(1)证明:∵∠BAE=∠BAD+45°,∠CDA=∠BAD+45°,
∴∠BAE=∠CDA(2分),
又∵∠B=∠C=45°,
∴△ABE∽△DCA(4分);
(2)解:∵△ABE∽△DCA,
∴
=
,
由依题意可知CA=BA=
,
∴
=
,
∴
=
,
∴
=
,
解得CE=
.
∴∠BAE=∠CDA(2分),
又∵∠B=∠C=45°,
∴△ABE∽△DCA(4分);
(2)解:∵△ABE∽△DCA,
∴
| BE |
| CA |
| BA |
| CD |
由依题意可知CA=BA=
| 2 |
∴
| BE | ||
|
| ||
| CD |
∴
| 2-CE | ||
|
| ||
| 2-BD |
∴
| 2-CE | ||
|
| ||
2-
|
解得CE=
| 2 |
| 3 |
点评:本题考查了等腰直角三角形的性质,相似三角形的判定与性质.关键是通过图形的旋转,将条件“相对集中”.

练习册系列答案
相关题目

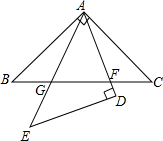 如图,在同一平面内,将两个全等的等腰直角三角形ABC和ADE摆放在一起,A为公共顶点,∠BAC=∠ADE=90°,若△ABC固定不动,△ADE绕点A旋转,AD、AE与边BC的交点分别为F、G(点G不与点B重合,点F不与点C重合).
如图,在同一平面内,将两个全等的等腰直角三角形ABC和ADE摆放在一起,A为公共顶点,∠BAC=∠ADE=90°,若△ABC固定不动,△ADE绕点A旋转,AD、AE与边BC的交点分别为F、G(点G不与点B重合,点F不与点C重合).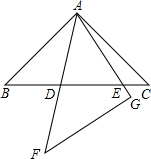 点分别为D、E(点D不与点B重合,点E不与点C重合),设BE=m,CD=n.
点分别为D、E(点D不与点B重合,点E不与点C重合),设BE=m,CD=n.
 ,求CE.
,求CE.