题目内容
平面上有若干个点，其中任意三点都不在同一直线上，将这些点分成三组，并按下面的规则用线段连接：①在同一组的任意两点间都没有线段连接；②不在同一组的任意两点间一定有线段连接。
（1） 若平面上恰好有9个点，且平均分成三组，那么平面上有多少条线段？
（2） 若平面上恰好有9个点，且点数分成2，3，4三组，那么平面上有多少条线段？
（3） 若平面上共有192条线段，那么平面上至少有多少个点？
（1）平面上恰好有9个点，且平均分成三组，每组3个点，其中每个点可以与另外两组的6个点连接，共有线段
（条）
（2）若平面
上恰好有9个点，且点数分成2，3，4三组，则平面上共有线段
（条）
（3）设第一组有
个点，第二组有
个点，第三组有
个点，则平面上共有线段
（条）
若保持第三组点数不变，将第一组中的一个点划归到第二组，则平面上线段的条数为
与原来线段的条数的差是
，即
当
时，
，此时平面上的线段条数不减少
当
时，
此时平面上的线段条数一定减少
由此可见，当平面上由点数较多的一组中划出一个点到点数较少的一组中时，平面上的线段条数不减少，所以当三组中点数一样多（或基本平均）时，平面上线段的条数最多
设三组中都有
个点，则线段条数为
解得
所以 平面上至少有24个点
练习册系列答案
相关题目
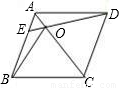
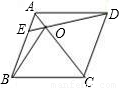
16、（1）如图，在菱形ABCD中，点E是AB上的一点，连接DE交AC于点O，连接BO，且∠AED=50°，则∠CBO
