题目内容
 如图,已知第一象限内的点A在反比例函数y=
如图,已知第一象限内的点A在反比例函数y=| 2 |
| x |
| k |
| x |
| 3 |
分析:作AC⊥x轴于点C,作BD⊥x轴于点D,易证△OBD∽△AOC,则面积的比等于相似比的平方,即tanA的平方,然后根据反比例函数中比例系数k的几何意义即可求解.
解答: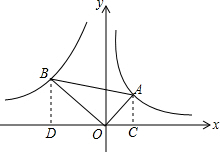 解:作AC⊥x轴于点C,作BD⊥x轴于点D.
解:作AC⊥x轴于点C,作BD⊥x轴于点D.
则∠BDO=∠ACO=90°,
则∠BOD+∠OBD=90°,
∵OA⊥OB,
∴∠BOD+∠AOC=90°,
∴∠BOD=∠AOC,
∴△OBD∽△AOC,
∴
=(
)2=(tanA)2=3,
又∵S△AOC=
×2=1,
∴S△OBD=3,
∴k=-6.
故选C.
 解:作AC⊥x轴于点C,作BD⊥x轴于点D.
解:作AC⊥x轴于点C,作BD⊥x轴于点D.则∠BDO=∠ACO=90°,
则∠BOD+∠OBD=90°,
∵OA⊥OB,
∴∠BOD+∠AOC=90°,
∴∠BOD=∠AOC,
∴△OBD∽△AOC,
∴
| S△OBD |
| S△AOC |
| OB |
| OA |
又∵S△AOC=
| 1 |
| 2 |
∴S△OBD=3,
∴k=-6.
故选C.
点评:本题考查了相似三角形的判定与性质,以及反比例函数的比例系数k的几何意义,正确作出辅助线求得两个三角形的面积的比是关键.

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案
相关题目
 (2013•乐山)如图,已知第一象限内的点A在反比例函数y=
(2013•乐山)如图,已知第一象限内的点A在反比例函数y=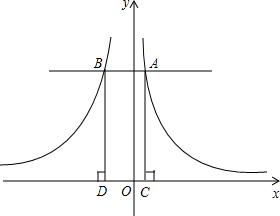 (2012•苏州)如图,已知第一象限内的图象是反比例函数y=
(2012•苏州)如图,已知第一象限内的图象是反比例函数y= 上,第二象限的点B在反比例函数
上,第二象限的点B在反比例函数 上,且OA⊥OB,
上,且OA⊥OB, ,则k的值为 (
)
,则k的值为 (
)

 图象的一个分支,第二象限内的图象是反比例函数
图象的一个分支,第二象限内的图象是反比例函数 图象的一个分支,在
图象的一个分支,在 轴上方有一条平行于
轴上方有一条平行于 与它们分别交于点A、B,过点A、B作
与它们分别交于点A、B,过点A、B作