Question

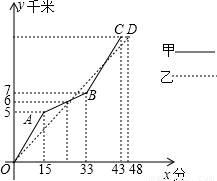
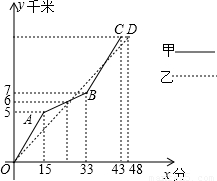
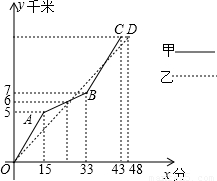
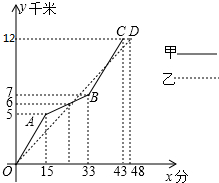下表表示甲、已两名选手在一次自行车越野赛中，路程y（千米）与时间x（分）变化的图象（全程）
根据图象完成下列问题：
（1）比赛开始多少分钟，两人第一次相遇；
（2）这次比赛全程是多少千米？
（3）求比赛开始多少分钟时，两人第二次相遇？

Answer 1

分析：两个函数图象交点的横坐标即为他们的相遇时间，观察图象，有两个交点，第一次在AB段，第二次在BC段，根据条件首先求出它们解析式，再把解析式分别联立，求出解，即得出相遇时间．
把x=48代入乙的解析式，得出比赛全程．

解答：解：（1）当15≤x≤33时，设y=kx+b，
∵点（15，5）（33，7）在此直线上，
∴

15k+b=5 33k+b=7

，解得

k= 1 9 b= 10 3

∴y=

1

9

x+

10

3

当y=6时，

1

9

x+

10

3

=6
x=24，即24分钟两人第一次相遇．

（2）对于乙选手来说，y是x的正比例函数，比例系数为

6

24

=

1

4

∴y=

1

4

x
当x=48时，y=12．故这次比赛全程是12千米．

（3）当33≤x≤43时，设y=mx+n
∵点（33，7），（43，12）在此直线上，
∴

33m+n=7 43m+n=12

，解得

m= 1 2 n=- 19 2

∴y=

1

2

x-

19

2

解方程组

y= 1 4 x y= 1 2 x- 19 2

，得

x=38 y= 19 2

，故在第38分钟时，两人第二次相遇．

点评：注意甲选手y与x的函数关系分三段，求相遇时间时，要看清是在哪一段，必须将对应段的函数解析式与乙的联立，求出的解才正确．