Question

【题目】把所有正奇数从小到大排列，并按如下规律分组：（1），（3，5，7），（9，11，13，15，17），（19，21，23，25，27，29，31），…，现有等式Am=（i，j）表示正奇数m是第i组第j个数（从左往右数），如A7=（2，3），则A2015=（ ）
A.（31，50）
B.（32，47）
C.（33，46）
D.（34，42）

Answer 1

【答案】B
【解析】方法一：
解：2015是第 =1008个数，
设2015在第n组，则1+3+5+7+…+（2n﹣1）≥1008，
即 ≥1008，
解得：n≥ ，
当n=31时，1+3+5+7+…+61=961；
当n=32时，1+3+5+7+…+63=1024；
故第1008个数在第32组，
第1024个数为：2×1024﹣1=2047，
第32组的第一个数为：2×962﹣1=1923，
则2015是（ +1）=47个数．
故A2015=（32，47）．
故选B．
方法二：
由观察可知，每行的第一个数及最后一行数呈二次函数，
即n=1，s=1；n=2，s=3，n=3，s=9，
n=1，s=1；n=2，s=7，n=3，s=17，
设s=an2+bn+c，
∴ ，∴ ，
∴第一行满足函数关系式：s=2n2﹣4n+3，
∴ ，∴ ，
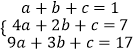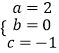∴最后一行满足的函数关系式：s=2n2﹣1，
∴2n2﹣4n+3＜2015＜2n2﹣1，
∴nmin=32，
取n=32代入第一行的函数关系式：s=2n2﹣4n+3，
∴s=1923，即第32行第一个数为1923，
∴j= =47，
∴A2015=（32，47）．
先计算出2015是第1008个数，然后判断第1008个数在第几组，再判断是这一组的第几个数即可．