题目内容
已知在直线上有n(n≥2的正整数)个点,每相邻两点间的距离为1,从左边第1起跳,且同时满足以下三条件:
①每次跳跃均尽可能最大;
②跳n次后必须回到第1个点;
③这n次跳跃将每个点全部到达.
设跳过的所路程之和为Sn,则S10= .
①每次跳跃均尽可能最大;
②跳n次后必须回到第1个点;
③这n次跳跃将每个点全部到达.
设跳过的所路程之和为Sn,则S10=
考点:规律型:图形的变化类
专题:
分析:首先认真读题,明确题意.按照题意要求列表(或画图),从中发现并总结出规律.注意:当n为偶数或奇数时,Sn的表达式有所不同.
解答:解:设这n个点从左向右依次编号为A1,A2,A3,…,An.
根据题意,n次跳跃的过程可以列表如下:
发现规律如下:
当n为偶数时,跳跃的路程为:Sn=(1+2+3+…+n-1)+
=
+
=
;
当n为奇数时,跳跃的路程为:Sn=(1+2+3+…+n-1)+
=
+
=
.
因此,当n=10时,跳跃的路程为:S10=
=50.
故答案为:50.
根据题意,n次跳跃的过程可以列表如下:
| 第n次跳跃 | 起点 | 终点 | 路程 | |||||
| 1 | A1 | An | n-1 | |||||
| 2 | An | A2 | n-2 | |||||
| 3 | A2 | An-1 | n-3 | |||||
| … | … | … | … | |||||
| n-1 | n为偶数 | A
|
A
|
1 | ||||
| n为奇数 | A
|
A
|
1 | |||||
| n | n为偶数 | A
|
A1 |
| ||||
| n为奇数 | A
|
A1 |
| |||||
当n为偶数时,跳跃的路程为:Sn=(1+2+3+…+n-1)+
| n |
| 2 |
| n(n-1) |
| 2 |
| n |
| 2 |
| n2 |
| 2 |
当n为奇数时,跳跃的路程为:Sn=(1+2+3+…+n-1)+
| n-1 |
| 2 |
| n(n-1) |
| 2 |
| n-1 |
| 2 |
| n2-1 |
| 2 |
因此,当n=10时,跳跃的路程为:S10=
| n2 |
| 2 |
故答案为:50.
点评:此题主要考查了图形变化规律,比较抽象.列表发现跳跃运动规律是解题的关键,同学们也可以自行画出图形予以验证.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
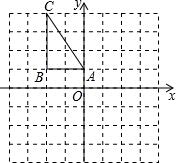 如图,在平面直角坐标系中,△ABC的三个顶点的坐标分别为A(0,1),B(-2,1),C(-2,4).
如图,在平面直角坐标系中,△ABC的三个顶点的坐标分别为A(0,1),B(-2,1),C(-2,4). 一副三角板如图放置,若∠1=90°,则∠2的度数为
一副三角板如图放置,若∠1=90°,则∠2的度数为