题目内容
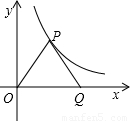
(2002•太原)如图,△OPQ的边长为2的等边三角形,若反比例函数的图象过点P,则它的关系式是 .
【答案】分析:根据△OPQ的边长为2可求P点坐标,再设y= ,把点P代入即可求得k,从而求出关系式.
,把点P代入即可求得k,从而求出关系式.
解答: 解:过点P作PA⊥OQ于A,
解:过点P作PA⊥OQ于A,
∵△OPQ的边长为2的等边三角形,
∴OP=2,OA=1,
∴PA= =
=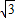 ,
,
∴P点坐标为(1, )
)
设y= ,把点P代入得,k=
,把点P代入得,k= ,
,
∴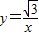 (x>0).
(x>0).
点评:主要考查了用待定系数法求反比例函数的解析式和反比例函数系数k的几何意义.反比例函数系数k的几何意义为:反比例函数图象上的点的横纵坐标之积是定值k,同时|k|也是该点到两坐标轴的垂线段与两坐标轴围成的矩形面积.本题要注意在实际意义中要考虑x的取值范围.
 ,把点P代入即可求得k,从而求出关系式.
,把点P代入即可求得k,从而求出关系式.解答:
 解:过点P作PA⊥OQ于A,
解:过点P作PA⊥OQ于A,∵△OPQ的边长为2的等边三角形,
∴OP=2,OA=1,
∴PA=
 =
=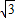 ,
,∴P点坐标为(1,
 )
)设y=
 ,把点P代入得,k=
,把点P代入得,k= ,
,∴
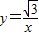 (x>0).
(x>0).点评:主要考查了用待定系数法求反比例函数的解析式和反比例函数系数k的几何意义.反比例函数系数k的几何意义为:反比例函数图象上的点的横纵坐标之积是定值k,同时|k|也是该点到两坐标轴的垂线段与两坐标轴围成的矩形面积.本题要注意在实际意义中要考虑x的取值范围.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目