题目内容
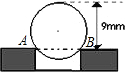如图，工程上常用钢珠来测量零件上小孔的直径，假设钢珠的直径是12毫米，测得钢珠顶端离零件表面的距离为9毫米，则这个小孔的直径AB是分析：已知钢珠的直径是12毫米，本题是有关圆的半径，弦长，弦心距之间的运算，通常是利用垂径定理，转化为解直角三角形问题．
解答：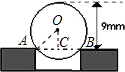
解：连接OA，通过圆心O，作弦AB的垂线交AB于C
则在Rt△OAC中，OA=6mm，OC=9-6=3mm
AC2+OC2=OA2，即AC2+32=62，
∴AC=3
mm
∴AB=6
mm．
解：连接OA，通过圆心O，作弦AB的垂线交AB于C则在Rt△OAC中，OA=6mm，OC=9-6=3mm
AC2+OC2=OA2，即AC2+32=62，
∴AC=3
| 3 |
∴AB=6
| 3 |
点评：有关圆的半径，弧长，弦长之间的计算一般是转化为解直角三角形．
练习册系列答案
相关题目
如图，工程上常用钢珠来测量零件上小圆孔的宽口，假设钢珠的直径是10cm，测得钢珠顶端离零件表面的距离为8cm，则这个小圆孔的宽口AB的长度为多少？
毫米．
