题目内容
(2005•漳州)某公司有员工50人,为了提高经济效益,决定引进一条新的生产线并从现有员工中抽调一部分员工到新的生产线上工作,经调查发现:分工后,留在原生产线上工作的员工每月人均产值提高40%;到新生产线上工作的员工每月人均产值为原来的3倍,设抽调x人到新生产线上工作.(1)填空:若分工前员工每月的人均产值为a元,则分工后,留在原生产线上工作的员工每月人均产值是______元,每月的总产值是______元;到新生产线上工作的员工每月人均产值是______元,每月的总产值是______元;
(2)分工后,若留在原生产线上的员工每月生产的总产值不少于分工前原生产线每月生产的总产值;而且新生产线每月生产的总产值又不少于分工前生产线每月生产的总产值的一半.问:抽调的人数应该在什么范围?
【答案】分析:(1)因为留在原生产线上工作的员工每月人均产值提高40%;到新生产线上工作的员工每月人均产值为原来的3倍,设抽调x人到新生产线上工作,所以留在原生产线上工作的员工每月人均产值是(1+40%)a,每月的总产值是(50-x)(1+40%)a元;到新生产线上工作的员工每月人均产值是3a元,每月的总产值是3ax元;
(2)因为留在原生产线上的员工每月生产的总产值不少于分工前原生产线每月生产的总产值;而且新生产线每月生产的总产值又不少于分工前生产线每月生产的总产值的一半,所以有由题可得不等式组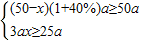 (其中a>0),解之即可.
(其中a>0),解之即可.
解答:解:(1)根据题意填空:(1+40%)a,(50-x)(1+40%)a,3a,3ax.
(2)由题可得不等式组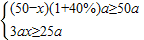 (其中a>0)
(其中a>0)
解得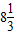 ≤x≤14
≤x≤14
由于x只能取正整数,
所以抽调的人数应在9-14人之间(包括9人和14人).
点评:本题考查一元一次不等式组的应用,将现实生活中的事件与数学思想联系起来,读懂题列出不等式关系式即可求解.准确的找到不等关系列不等式是解题的关键.注意本题的不等关系为:留在原生产线上的员工每月生产的总产值不少于分工前原生产线每月生产的总产值;新生产线每月生产的总产值又不少于分工前生产线每月生产的总产值的一半.
(2)因为留在原生产线上的员工每月生产的总产值不少于分工前原生产线每月生产的总产值;而且新生产线每月生产的总产值又不少于分工前生产线每月生产的总产值的一半,所以有由题可得不等式组
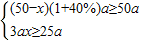 (其中a>0),解之即可.
(其中a>0),解之即可.解答:解:(1)根据题意填空:(1+40%)a,(50-x)(1+40%)a,3a,3ax.
(2)由题可得不等式组
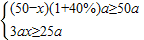 (其中a>0)
(其中a>0)解得
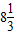 ≤x≤14
≤x≤14
由于x只能取正整数,
所以抽调的人数应在9-14人之间(包括9人和14人).
点评:本题考查一元一次不等式组的应用,将现实生活中的事件与数学思想联系起来,读懂题列出不等式关系式即可求解.准确的找到不等关系列不等式是解题的关键.注意本题的不等关系为:留在原生产线上的员工每月生产的总产值不少于分工前原生产线每月生产的总产值;新生产线每月生产的总产值又不少于分工前生产线每月生产的总产值的一半.

练习册系列答案
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案
相关题目
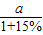 元
元