题目内容
如图,河坝横断面迎水坡AB的坡比是1∶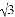 (坡比是坡面的铅直高度BC与水平宽度AC之比),坝高BC=3 m,则坡面AB的长度是( )
(坡比是坡面的铅直高度BC与水平宽度AC之比),坝高BC=3 m,则坡面AB的长度是( )

A. 9 m B. 6 m C. 6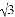 m D. 3
m D. 3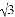 m
m
练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
题目内容
如图,河坝横断面迎水坡AB的坡比是1∶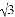 (坡比是坡面的铅直高度BC与水平宽度AC之比),坝高BC=3 m,则坡面AB的长度是( )
(坡比是坡面的铅直高度BC与水平宽度AC之比),坝高BC=3 m,则坡面AB的长度是( )

A. 9 m B. 6 m C. 6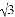 m D. 3
m D. 3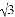 m
m
 口算题天天练系列答案
口算题天天练系列答案